|

|
How
to Solve Word Problems Programmatically
|
Chapter
4
|
|
|

|
|
|
|
Chapter 4. Unit Systems
|
|
|
|
|
|
|
|
|
4.1
|
US System
|

|
|
|
|
Abbrev.
|
Name
|
Derivation
|
Illustrative Examples
|
|
|
|
|
Length Dimension
|
|
in
|
inch
|
|
between two knuckles of an average finger
|
|
ft
|
foot
|
12 in
|
average man's
foot
|
|
yd
|
yard
|
3 ft
|
from floor to
standard door knob
|
|
mi
|
mile
|
5280 ft
|
four times
around a traditional track field
|
|
|
|
|
Weight Dimension
|
|
oz
|
ounce
|
|
one-fourth cube
of butter
|
|
lb
|
pounds
|
16 oz
|
four cubes of
butter
|
|
ton
|
tons
|
2000 ton
|
a lot of butter
|
|
|
|
|
Area Dimension
|
|
in2
|
square inch
|
|
square that
surrounds a quarter
|
|
ft2
|
square feet
|
144 in2
|
average size of
floor tile
|
|
yd2
|
square yard
|
9 ft2
|
an average card
table
|
|
acre
|
acre
|
4840 yd2
|
just over 90
yards of a football field
|
|
section
|
section
|
640 acres
|
1 square mile
|
|
township
|
township
|
36 sections
|
6 miles by 6
miles
|
|
|
|
|
Volume Dimension
|
|
tsp
|
teaspoon
|
|
standard spoon
size
|
|
tbsp
|
tablespoon
|
3 tsp
|
large spoon size
|
|
floz
|
fluid ounce
|
6 tsp
|
2 large spoon
sizes
|
|
cup
|
cup
|
8 floz
|
small size
carton of milk
|
|
pt
|
pint
|
2 cup
|
standard size of
carton for cream
|
|
qt
|
quart
|
2 pt
|
medium size of
carton for milk
|
|
gal
|
gallon
|
4 qt
|
large size of
carton for milk
|
|
|
|
|
|
Common US Units
|
|
|
4.2
|
Metric System
|

|
|
|
|
Abbrev.
|
Name
|
Derivation
|
Illustrative Examples
|
|
|
|
|
Length Dimension
|
|
mm
|
meter
|
|
width of one dime
|
|
cm
|
centimeter
|
10 mm
|
width of ten
dimes
|
|
m
|
meter
|
10 cm
|
one half height
of 6 foot 6 in basketball player
|
|
km
|
kilometer
|
10 m
|
almost three
times around high school track field
|
|
|
|
|
Weight Dimension
|
|
mg
|
milligram
|
|
|
|
g
|
gram
|
1000 mg
|
water in small
thumbnail (1 ml)
|
|
kg
|
kilogram
|
1000 g
|
water in a
common size of bottled water (1 liter)
|
|
tonne
|
metric ton
|
1000 kg
|
water in a cubic
meter container
|
|
|
|
|
Area Dimension
|
|
mm2
|
square
millimeter
|
|
size of surface
of a pin head
|
|
cm2
|
square
centimeter
|
100 mm2
|
size of a small
fingernail
|
|
dm2
|
square
deciimeter
|
100 cm2
|
size of a small
fingernail
|
|
m2
|
square meter
|
100 dm2
|
just larger than
an average card table
|
|
km2
|
square kilometer
|
1,000,000 m2
|
about one third
of a square mile
|
|
barn
|
barn
|
10-28 m2
|
cross section of nuclei of atom
|
|
|
|
|
Volume Dimension
|
|
mL
|
milliliter
|
1 cm3
|
small thumbnail
of water
|
|
L
|
liter
|
1000 mL
|
common size of
bottled water
|
|
|
|
|
|
Common Metric
Units
The metric system emphasizes the use of the decimal system
of numbers. Notice that the
derivations of related units come from factors of 10. This makes unit conversions and
calculations more convenient, it has become an international standard,
especially for scientific publications.
Common conversions from other systems (including the US System) to the
metric system can be found at websites such as:
http://www.convertit.com/Go/Bioresearchonline/Measurement/Units.ASP
(Conversions)
http://www.chezcrowe.com/conv_app.htm
(Conversion)
|
|
|
4.3
|
Unit Prefixes
|

|
|
|
|
Name
|
Prefix
|
Unit Identity
|
Inverse Unit Identity
|
|
yotta
|
Y
|
10^24 m/Ym
|
10^-24 Ym/m
|
|
zetta
|
Z
|
10^21 m/Zm
|
10^-21 Zm/m
|
|
exa
|
E
|
10^18 m/Em
|
10^-18 Em/m
|
|
peta
|
P
|
10^15 m/Pm
|
10^-15 Pm/m
|
|
tera
|
T
|
10^12 m/Tm
|
10^-12 Tm/m
|
|
giga
|
G
|
10^9 m/Gm
|
10^-9 Gm/m
|
|
mega
|
M
|
10^6 m/Mm
|
10^-6 Mm/m
|
|
kilo
|
k
|
10^3 m/km
|
10^-3 km/m
|
|
hecto
|
h
|
100 m/hm
|
.01 hm/m
|
|
deca
|
da
|
10 m/dam
|
.1 dam/m
|
|
1
|
|
|
|
|
deci
|
d
|
0.1 m/dm
|
10 dm/m
|
|
centi
|
c
|
0.01 m/cm
|
100 cm/m
|
|
milli
|
m
|
10^-3 m/mm
|
10^3 mm/m
|
|
micro
|
µ
|
10^-6 m/µm
|
10^6 µm/m
|
|
nano
|
n
|
10^-9 m/nm
|
10^9 nm/m
|
|
pico
|
p
|
10^-12 m/pm
|
10^12 pm/m
|
|
femto
|
f
|
10^-15 m/fm
|
10^15 fm/m
|
|
atto
|
a
|
10^-18 m/am
|
10^18 am/m
|
|
zepto
|
z
|
10^-21 m/zm
|
10^21 zm/m
|
|
yocto
|
y
|
10^-24 m/ym |
10^24 ym/m |
|
Unit Prefixes
|
Since the metric system is conveniently based on the
decimal system, we can use prefixes to create units related to a given unit
by factors of ten. For example, a
kilogram (using the prefix "kilo") is a new unit derived from the
unit gram by multiplying by 1000. The
above table gives the unit identities that convert between such units.
|
|
|
4.4
|
Using Natural Phenomena
|

|
|
|
|
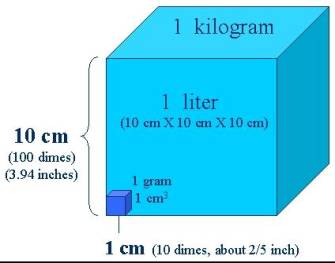
[meter~Length(Thing)]
Calculated from curvature of the earth
|

|
|
|
[liter~Volume(Thing)]
Cubic decimeter
[kilogram~Mass(Thing)]
Liter of water
[gram~Mass(Thing)]
Cubic centimeter of water
|
The metric system begins with a definition of the unit "meter" for the
dimension "length" based on the natural phenomena of the curvature
of the earth which a person can determine using trigonometry to a reasonable
amount of accuracy anywhere on the earth.
Later scientists gained more accuracy by using natural concepts of
light. The choice of meter came close
to the commonly used unit of a yard.
The metric system defines the unit "liter" for
the dimension "volume" as a cubic decimeter. This particular choice of how a liter
depends on a meter results in a volume unit close to the unit
"quart". Now using the
natural phenomena of water, the metric system defines the unit
"kilogram" of the dimension "mass" as the mass of water contained
in one liter. This means that a gram
of water fills a cube having one-centimeter edges.
|
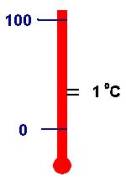
Water is an abundantly available phenomena. In addition to the mass unit Liter, we
use water to define units of temperature (degrees Centigrade) and energy
(calories). Following the decimal
goals of the metric system, the freezing point of water determines zero
degrees Centigrade and the boiling point of water determines 100 degrees
Centigrade. The unit kelvin (K)
uses the same increment (1°C = 1 K) but
shifts the value 0 to absolute zero. Originally, scientists measured energy with the unit calorie
defined as the amount of energy to raise one gram of water one degree
Centigrade.
|
|
Today, they use the unit joules to measure energy and the
relationship between calories and joules for a particular substance (in
addition to just water) is the specific heat of that substance. For more information see http://library.thinkquest.org/C004970/thermo/specific.htm?tqskip1=1
|
|
|
4.5
|
SI System (System International)
|

|
|
|
|
Abbreviation
|
Unit
|
Dimension
|
|
|
SEVEN
BASE UNITS
|
|
|
m
|
meter
|
length
|
|
kg
|
kilogram
|
mass
|
|
s
|
second
|
time
|
|
A
|
ampere
|
electric current
|
|
K
|
kelvin
|
temperature
|
|
mol
|
mole
|
amount of matter
|
|
cd
|
candela
|
luminous intensity
|
|
|
ANGLE
UNITS
|
|
|
rad
|
radians
|
plane angle
|
|
sr
|
steradians
|
solid angle
|
|
|
DERIVED
UNITS
|
|
|
m2
|
meters squared
|
area
|
|
m3
|
meters cubed
|
volume
|
|
m/s
|
meters per second
|
velocity
|
|
m/s2
|
meters per second squared
|
acceleration
|
|
rad/s
|
radians per second
|
angular velocity
|
|
rad/s2
|
radians per second squared
|
angular acceleration
|
|
kg/m3
|
kilograms per meters cubed
|
density
|
|
cd/m2
|
candela per meter squared
|
luminance
|
|
A/m
|
ampere per meter
|
magnetic field strength
|
|
|
DERIVED
UNITS
WITH NEW
SYMBOLS
|
|
|
N = kg*m/s2
|
newton
|
force
|
|
Pa = N/m2
|
pascal
|
pressure
|
|
J = N*m
|
joule
|
quantity of energy
|
|
W = J/s
|
watt
|
power
|
|
V = W/A
|
volt
|
voltage
|
|
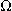 = V/A = V/A
|
ohm
|
electric resistance
|
|
C = A*s
|
coulomb
|
electric charge
|
|
F = C/V
|
farad
|
electric capacitance
|
|
Hz = cycles/s
|
hertz
|
frequency
|
|
Wb = V*s
|
weber
|
magnetic flux
|
|
T = Wb/m2
|
tesla
|
magnetic flux density
|
|
H = Wb/A
|
henry
|
inductance
|
|
lm = cd*sr
|
lumen
|
flux of light
|
|
lx = lm/m2
|
lux
|
illumination
|
|
|
|
|
|
SI System
|
Common SI Units
The seven base units create the foundation from which we
derive all other SI units. Notice
that each unit combines previously defined units using simple division and
multiplications. In fact, most of
units relate back to the first three base units (meters, kilograms, and
seconds) through simple algebraic substitutions. A 75 watt light bulb refers to a 75 kg*m2/s3
light bulb where we have the chain of derivations: W=J/s=N*m/s= (kg*m/s2)*m/s=
kg*m2/s3. Even
the base unit "ampere" relates back to the first three units
through the relationship between magnetic forces and electronic currents;
briefly, an ampere represents the amount of current in two straight parallel
wires set 1 meter apart to produce a magnetic force of 2*10^-7 newtons. (See http://physics.nist.gov/cuu/Units/units.html)
The angle units represent supplementary units that use
length and area to measure plane and solid angles respectfully. You can find more information concerning
the SI System of Units at sites such as:
http://metre.info/ (Extensive
Details of SI or Modern Metric System)
http://www.metricmethods.com/metricmoments.html
|
|
|
4.6
|
UM System (Unified Math)
|

|
|
|
|
Abbreviation
|
Unit
|
Dimension
|
|
|
NINE BASE
UNITS
|
|
|
m
|
meter
|
length
|
|
kg
|
kilogram
|
mass
|
|
s
|
second
|
time
|
|
A
|
ampere
|
electric current
|
|
K
|
kelvin
|
temperature
|
|
mol
|
mole
|
amount of matter
|
|
cd
|
candela
|
luminous intensity
|
|
dol
|
dollar
|
monetary value
|
|
ins
|
instance
|
occurance
|
|
|
EXAMPLE
DERIVED
UNITS
|
|
|
dol/m
|
dollars per lineal meter
|
price per length
|
|
ins/s
|
instance per second
|
event frequency
|
|
s/ins
|
seconds per instance
|
duration
|
|
dol/ins
|
dollars per instance
|
price
|
|
dol/unit
|
dollars per unit
|
unit price
|
|
UM System
|
The Unified Math® system of units adds two new base units
to the SI system, allowing us to handle business and statistical problems.
|
|
|
4.7
|
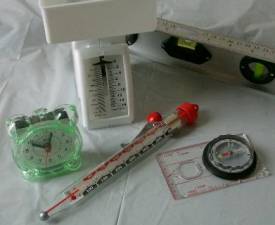
Measuring Instruments
|

|
|
|
|
|
|
4.8
|
Calibration
|

|
|
|
The process of calibrating a measuring instrument often
involves adjusting the size of one dimension to match a predefined value of
another dimension. Take for example a
kitchen scale that measures weight based on a spring inside the measuring
instrument. Such a device quite often
has a knob (shown on the back of the one above) that allows the user to
adjust the pointer connected to the spring so that it lines up with the 0
mark on the scale.
|
|
|
4.9
|
Impact of Units on Formulas
|

|
|
|
|
|
Distance = Velocity * Time
d = v * t
(if d miles, v miles/hour, t hour)
d = v * t / 60 (if
d miles, v miles/hour, t minutes)
d = 1.61 * v * t (if d
kilometers, v miles/hour, t hour)
|
Units can change form of
equation
|
The choice of units determines the form of the
equation. It is not sufficient just
to say that distance equals the velocity (speed) times the time. We need to also specify the units of each
quantity in the equation.
|
|
|
|
4.10
|
Activities and Explorations
|

|
|
|
|
|
Activities:
|
|
Play “Unit Scavenger Hunt” game
Compile Lists of Measuring Instruments
Have teams create a list of measuring instruments. They can do this by browsing through the
Internet or retail stores making a list of measuring instruments and the
scales encountered.
|
Explorations:
Exercises:
|
|
Do Related Problems In Your Textbook
|
|
|
Home
| Top
Copyright ©
2004 Dr. Ranel E. Erickson
|