Chapter 5.  Number Lines

A number line consists of a line having equally spaced tick marks with sequential numbers assigned to them.  The distance between each mark represents the (abstract) unit.  We use number lines to visualize many mathematical concepts   A specific point on such a line visually represents a number such as the number 8 above. 

In essence, the tick marks provide an abstract representation of a unit.  We can study many concepts of a number line, and these concepts will apply to many real applications involving measurements.

We call the set of points between two points an interval or line segment.  The notation [5,12] represents the interval between the numbers 5 and 12 inclusive.  If an end point (such as 12) does not belong to the interval, then a parenthesis “)“ replaces the brace “]“.   In this instance, the interval [5,12) represents the set of numbers between 5 and 12, including 5 and all numbers to 12 but not 12.

Remember how Euclid focused on the construction of a line between two points.  Modern math uses number lines to determine the relative position of points on a line between to points. 

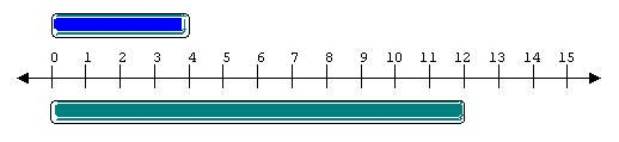
A number line can show how things (as well as numbers) relate to each other, no matter what type of unit we use; we can compare the same number line to two objects to determine a relationship between them.  For example, the length of two boards relate through a number line, even though we have not yet assigned a specific unit (such as a foot) to the interval [0,1].  The above illustration allows us to conclude that the length of the first bar has a greater length than the second bar, about 3 times greater. 

Number lines allow us visualize the comparison numbers.  We say that a number 12 has a greater value than a number 5 if 12 lies to the right of 5 on the above number line.  The number line visually represents the fact that if we start to count from 1 we will encounter the number 5 before the number 12.  The greater than symbol “>” in the statement 12 > 5 expresses this concept.  Similarly, the less than symbol “<” expresses the opposite relationship, namely, 5 < 12.

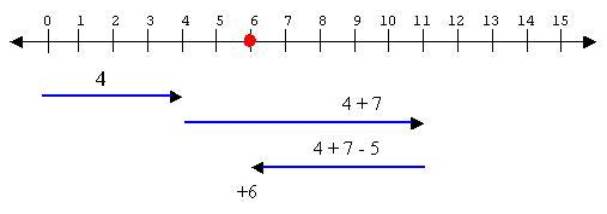
Let us visualize the arithmetic operations of addition and subtraction on the number line.  To add 4 to 7 we move four (4) units to the right of the point 7 arriving at the point 11.  Place your left index finger on 4 and move your right index finger to the right counting 7 until you reach the number 11.  To subtract 5, then, move your right finger five units to the left.  Where did you end up?  Six (6).  Great!  Hence the expression  4 + 7 - 5  = 6. 

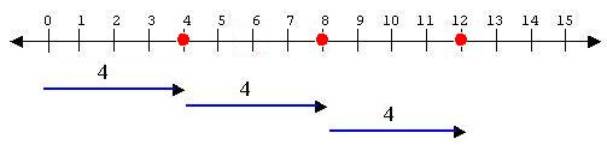
Similarly, we can use number lines to visualize the operations of multiplication.  Consider, for example, 3 * 4 = 12 represented by moving 4 units to the right 3 times.

The operator symbols determine how we manipulate numbers.  The language of mathematics contains many symbols that capture ideas in brief but consistent statements.  For example, the famous Greek mathematician, Pythagoras, summarized the relationships between the lengths (a, b, and c) of the sides of a right triangle in the now famous symbolic statement c² = a² + b².  He stated and proved this formula over 2,500 years ago not using algebra, but from visual geometric diagrams.  Number lines provide us with on of the most effective ways to visualize many concepts in mathematics

For many centuries after great mathematicians like Euclid and Archimedes, people still only used numbers greater than or equal to 0.  They could not subtract 6 from 3.  To handle this, they needed to introduce a new kind of number, a negative number.  Today, in the language of mathematics, the number zero (0) represents the additive identity because 5 + 0 = 5.  On the number line, the point representing a number remains fixed when adding 0.   The additive inverse (or negative) of a natural number (like 5) creates a new kind of number (written -5) that when added to that given number 5 results in 0.  We call the symbol “-“ the negation operator, instead of a minus representing subtraction, and place it in front of a number to operate on it resulting in the negative of that number.  The set of integers consists of the set of all whole numbers and their additive inverses. 

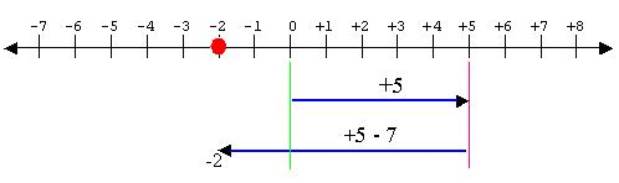
Number lines can illustrate operations involving negative numbers.  As shown above, on adding a -7 to a 5 we get a -2.  By definition, the inverse of the inverse results in the original integer:  -(-7) = 7.   Similarly, the syntax of the mathematical language has specific rules for the multiplication of signed numbers.  We get a positive sign when multiplying two numbers with the same signs; otherwise, we get a negative sign.

Similar addition, the number 1 plays the role of the multiplicative identity (4 * 1 = 4), and the multiplicative inverse of a number (like 4) creates a new kind of number (written as ¼ or 4^-1).   When the original number 4 is multiplied by the multiplicative inverse ¼, the answer results in 1 written mathematically as 4 * ¼ = 1.  When graphed, the multiplicative inverse of any natural number (1, 2, 3, …) is always found between the points 0 and 1 on the number line.

How do we create all types of fractions?  By multiplying these multiplicative inverse numbers with integer numbers we obtain results like 2/3, 20/43, 5/2, -8/3 and -10/15.    As discussed in previous chapters, the top number is the numerator and the bottom number is the denominator.  In a proper fraction the numerator has a value less than the denominator.

In the decimal system, fractions find their representation with placeholders designated by digit places to the right of the decimal point, called the fractional part of the decimal number.  In the above example, the digits 4, 2, and 5 fall into positions that relate to the fractions 1/10, 1/100, and 1/1000 respectively.  To convert this decimal part to a fraction, place the digits 425 located to the right of the decimal over the number 1000 whose inverse thousandths (1/1000) corresponds to the last place-holder (3rd position to the right) yielding, in this case, 425/1000.  Basically, 425 * 1/1000 yields the 425/1000. 

The set of rational numbers consist of all fractions.  When expressed as decimals, they have a special property.  On carrying out the division of a fraction, the resulting decimal number may have a finite or an infinite number of decimal places to the right.  For example, ¼ = .25 has a finite number but 1/3 = .3333333… has an infinite number.   But mathematicians have proven that all fractions result in decimal numbers with a sequence of numbers that repeat.  The 3 repeats in calculating 1/3.  Can you see the repeating sequence of numbers when dividing 3 by 7?

Other calculations result in numbers that have digits to the right of the decimal that do not repeat regardless of how many digits we compute.  Calculating the ratio of the diameter to the circumference of a circle ( p = 3.1415926535897932384626433832795…) results in no pattern.   Odd, but true.  This famous and anciently studied number does not have an exact fractional representation. The square root of  2 (=1.414213562373095048801688724209…) provides another example where the decimal digits never repeat themselves in a pattern.  We call these new kinds of number irrational numbers.

The combination of irrational and rational numbers determines the set of real numbers.  In general, we can express a real number as a decimal number with any number of digits to the right of the decimal number (including an infinite number of non-repeating digits).   We often refer to a number line as a real number line to indicate that the line represents a continuum of real numbers.

In order to measure and relate phenomena as large as distant galaxies and as small as atoms, we need a more convenient way to write large decimal numbers such as 48,200,000 or small decimal numbers such as 0.0000231.  Scientific notation does that using several different styles as indicated above, but in each of these, the number in the exponent indicates how many digits the decimal must move to create the decimal number.  We can interpret each movement of the decimal toward the right as increasing the size of a thing by a power of 10.  So an exponent of 7 would indicate that the thing has been increased 10 fold seven times resulting in a factor of 10,000,000 times.  Similarly, a movement toward the left would indicate a reduction of 10 fold per each digit moved.

We can create a visual image of a scaled dimension by assigning a particular unit to the interval [0,1] and specifying a dimension of a thing that the real number line measures.  Suppose, for example, that we desire to measure the height of a kitchen cabinet.  Then the above diagram illustrates the scaled dimension [ft~Height(Cabinet)].  We would plot a unified number such as 7 [ft~Height(Cabinet)] as the point at the tick mark 7 on the scaled dimension graph above.

Modern mathematics uses the concepts of sets as its foundation.  This section reviews some of the basic vocabulary words, symbols and concepts associated with sets.

A set comprises a group of things called members.  We characterize a set by using a specific list if its members or by stating the criteria that determine whether or not an object belongs to that set.   Traditionally, capital letters such as A, B, C, etc., designate sets and then braces { … } enclose the members (or criteria) of the set.   You can choose any symbol that you like to name the set. The ellipsis (…)--three dots--indicate that the sequential pattern continues.  If the pattern stops (for example at z for the alphabet and 9 for the digits), then the terminating object or idea follows the ellipsis.  If a set does not terminate, then we call it an infinite set, and it has aninfinite number of members.  The following symbols help us to communicate ideas about sets:

The above table contains new vocabulary words that help us relate the objects and ideas around us.  Briefly, we define a set B as a subset of A if all the members of B belong to A.  We define a set A as a superset of A if A has B as a subset.  As an opposite of subset, we say that a superset A contains B. The empty set (or null set) designates a set with no members.  By definition, any set contains the empty set.  We define a set C as the intersection of two sets A and B if each member of C belongs to both the sets A and B.  We define a set C as the union of two sets A and B if each member of C belongs to either set A or set B.

Sets play an important role in the mathematical language of numbers.  In this book, when we solve for solutions of a given word problem, we seek the set of values, called the solution set, that satisfy the criteria described in the problem.  The solution set may consist of no members, one member, or multiple members (even an infinite number of members). 

Unified Math®  introduces a new kind of number, called the unified number.  I attaches the meaning of a number with the number resulting in an entity that we treat as a complete object.  This object participates in special mathematical operations.  For example, the multiplication of two unified numbers depends in general on the integral, a calculus concept that we will visualize later as the area under the curve that relates the two unified numbers.

Unified Math®  uses set theory to establish the foundation of unified numbers.   For more information, check out the Foundations of Unified Math®  Appendix.

 Activities:

Explorations:

Exercises:

Home  |  Top

Copyright © 2004  Dr. Ranel E. Erickson