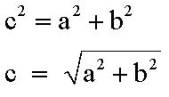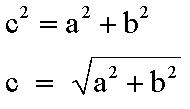|

|
How
to Solve Word Problems Programmatically
|
Chapter
7
|
|
|

|
|
|
|
Chapter 7.
Relationships
|
|
|
|
|
|
|
|
|
7.1
|
System of Abstract Things
|

|
|
|
|
|
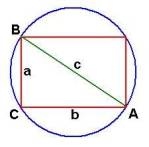
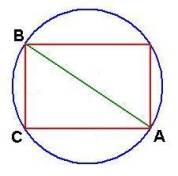
System of Abstract Things:
Circle
Rectangle
Line
Points A, B, and C
|
A system of abstract things contains things that have
common parts or related dimensions.
Above we have an abstract system of things including of a line between
two opposite corner points (A and B) of a rectangle that lie on a
circle. Even though we may describe a
few initial things in a system, there usually exist many other interrelated
things and subthings. In this
abstract system, we can further identify two adjacent right triangles and
various arc segments. We will also
say "abstract system" to refer to a system of abstract things.
|
|
|
7.2
|
Relating Quantities
|

|
|
|
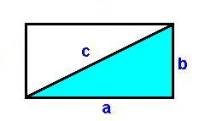
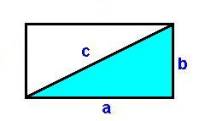
The quantities a, b, and c of the dimensions SideA, SideB,
and SideC of the thing TriangleABC relate to each other through the
Pythagorean theorem for right triangles.
If these three quantities were to appear in a word problem, we can
then use this relationship to relate on of these sides to the other two. For instance, we may relate the third side
entered into the meaning table with the other two sides.
|
Qty
|
Value
|
Meaning
|
Relationship
|
|
q1
|
a
|
[m~SideA(TriangleABC)]
|
|
|
q2
|
b
|
[m~SideB(TriangleABC)]
|
|
|
q3
|
c
|
[m~SideC(TriangleABC)]
|
sqrt(q1^2+q2^2)
|
|
|
|
7.3
|
Defining Dimensions
|

|
|
|
|
Qty
|
Value
|
Meaning
|
Relationship
|
|
q1
|
a
|
[m~SideA(TriangleABC)]
|
|
|
q2
|
b
|
[m~SideB(TriangleABC)]
|
|
|
q3
|
c
|
[m~SideC(TriangleABC)]
|
sqrt(q1^2+q2^2)
|
|
q4
|
d
|
[m~Diameter(Circle)]
|
q3
|
|
q5
|
p
|
[m~Perimeter(Rectangle)]
|
2*q1+2*q2
|
|
q6
|
q
|
[m~Perimeter(TriangleABC)]
|
q1+q2+q3
|
|
q7
|
C
|
[m~Circumference(Circle)]
|
π *q4
|
|
q8
|
r
|
[m~Radius(Circle)]
|
q4/2
|
|
q9
|
A
|
[m2~Area(Rectangle)]
|
q1*q2
|
|
q10
|
X
|
[m2~Area(TriangleABC)]
|
q1*q2/2
|
|
q11
|
Y
|
[m2~Area(Circle)]
|
p*q8^2
|
Other relationships come from the definition of new
dimensions. In such cases, a given
word (like diameter, perimeter, and circumference) determines appropriate
relationships. Notice how the
relationships entered into the above meaning table come from definition
formulas such as:
p=2*a+2*b
q= a+b+c
C= π * d
r= d/2
A= a*b
X= a*b/2
Y=p*r^2
Each of the entries in the meaning table illustrates an
additional dimension of a system consisting of a rectangle inscribed by a
circle introduced by relating it to previously defined dimension. In essence, the expressions placed in the
Relationship column of the meaning table come form the definition of the that
dimension. When formulating word
problems using Unified Math®, we will take this general approach of
introducing formulas as definitions of the meaning associated with the
quantities.
|
|
|
7.4
|
Unified Quantities in Abstract Systems
|

|
|
|
|
|
|
a
b
c
sqrt(a2+b2)
a+b+c
2*a+2*b
a*b
a*b/2
|
[m~Width(Rectangle)]
[m~Height(Rectangle)]
[m~Diagonal(Rectangle)]
[m~Hypotenuse(RightTriangle)]
[m~Perimeter(RightTriangle)]
[m~Perimeter(Rectangle)]
[m2~Area(Rectangle)]
[m2~Area(RightTriangle)]
|
Unified Quantity Expressions
in a
System of
Abstract
Things
|
|
|
|
7.5
|
Applying Abstract Systems
|

|
|
|
|
Qty
|
Value
|
Meaning
|
Relationship
|
|
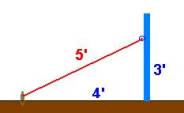
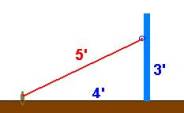
q1
|
c
|
[m~Length(Rope)]
|
sqrt(q2^2+q3^2)
|
|
q2
|
4
|
[m~LengthTo(Stake)]
|
|
|
q3
|
3
|
[m~Height(PoleRing)]
|
|
|
[m~LengthTo(Stake)]
[m~Height(PoleRing)]
[m~Length(Rope)]
|
[m~Width(RightTriangle)]
[m~Height(RightTriangle)]
[m~Hypotenuse(RightTriangle)]
|
|
Qty
|
Value
|
Meaning
|
Relationship
|
|
q1
|
c
|
[m~Hypotenuse(RightTriangle)]
|
sqrt(q2^2+q3^2)
|
|
q2
|
|
[m~Width(RightTriangle)]
|
|
|
q3
|
|
[m~Height(RightTriangle)]
|
|
|
|
|
7.6
|
State of a System
|

|
|
|
|
4
3
5
sqrt(42+32)
4+3+5
2*4+2*3
4*3
4*3/2
|
[m~Width(Rectangle)]
[m~Height(Rectangle)]
[m~Diagonal(Rectangle)]
[m~Hypotenuse(RightTriangle)]
[m~Perimeter(RightTriangle)]
[m~Perimeter(Rectangle)]
[m2~Area(Rectangle)]
[m2~Area(RightTriangle)]
|
a
b
c
sqrt(a2+b2)
a+b+c
2*a+2*b
a*b
a*b/2
|
|
|
|
7.7
|
Physical System
|

|
|
|
|
|
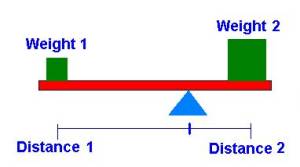
Principle of Balance:
w1 * d1 = w2 * d2
|
A fundamental relationship discovered by the Greek
mathematician Archimedes of Syracuse (around 250
BC) describes the relationship between things on a balance placed at
specific distances away from the center of the balance. The following unified quantities and
their relationship characterize this system:
|
Qty
|
Value
|
Meaning
|
Relationship
|
|
q1
|
w1
|
[kg~Weight(Thing1)]
|
|
|
q2
|
w2
|
[kg~Weight(Thing2)]
|
|
|
q3
|
d1
|
[m~LengthFromCenter(Thing1)]
|
|
|
q4
|
d2
|
[m~LengthFromCenter (Thing2)]
|
q1*q2/q3
|
|
|
|
7.8
|
Comparative Systems
|

|
|
|
|
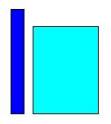
How do we determine if one thing is "greater"
than another? Is the rectangle on
the left "greater" than the one on the right? It depends on our choice of dimensions
that we compare. If we use the
dimension height to determine the meaning of "greater" then the
rectangle on the left is larger, even though it appears thinner with far
less area.
|
|
Comparing Two Things
|
Many words in the English language refer to comparisons,
many of which have opposites: thinner-smaller, colder-hotter,
heavier-lighter, top-bottom, etc.
What does it mean to be on "top"? The answer "a greater vertical length from the earth"
implies mathematical measurements and comparisons. These words translate into the abstract concepts of
"greater than" (>) and "less than" (<). Their use in word problems usually invokes
a measure of how much greater or how much less than, words that indicate
adding and subtracting. We consider
all such comparative words as mathematical vocabulary words. Such words usually lead to relationships
involving either an addition or a subtraction. Consider the following phrases:
|
|
sue is 2 inches
taller than john
the box weighs 10
pounds lighter than the lamp
today's temperatures
is 3 degrees higher than normal
|
The following unified quantities and their relationship
characterize these phrases:
|
Qty
|
Value
|
Meaning
|
Relationship
|
|
q1
|
j
|
[in~Height(John)]
|
|
|
q2
|
s
|
[in~Height(Sue)]
|
q1+2
|
|
q3
|
|
[lb~Weight(Lamp)]
|
|
|
q4
|
B
|
[lb~Weight(Box)]
|
q3-10
|
|
q5
|
N
|
[°F~Temperature(Normal)]
|
|
|
q6
|
N+3
|
[°F~Temperature(Today)]
|
|
|
|
|
7.9
|
Business Transaction Systems
|

|
|
|
|
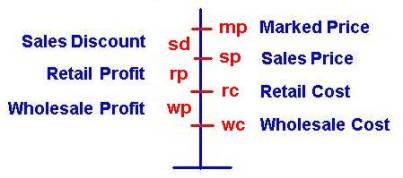
|
Relationships
in a Business
Transaction
|
|
Qty
|
Value
|
Meaning
|
Relationship
|
|
q1
|
mp
|
[dol~Marked Price(Thing)]
|
|
|
q2
|
sp
|
[dol~Sale Price(Thing)]
|
|
|
q3
|
|
[dol~Retail Cost(Thing)]
|
|
|
q4
|
wc
|
[dol~Wholesale Cost(Thing)]
|
|
|
q5
|
sd
|
[dol~Sales Discount(Thing)]
|
q1-q2
|
|
q6
|
rp
|
[dol~Retail Profit(Thing)]
|
q2-q3
|
|
q7
|
wp
|
[dol~Wholesale Profit(Thing)]
|
q3-q4
|
|
q8
|
a
|
[ins~Occurrence(Thing)]
|
|
|
q9
|
tc
|
[dol~Total Cost(Thing)]
|
q8*q2
|
|
|
|
7.10
|
Finance Systems
|

|
|
|
|
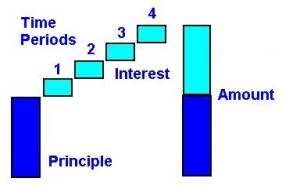
|
Relationships
in a Simple Interest
Loan
|
|
Qty
|
Value
|
Meaning
|
Relationship
|
|
q1
|
p
|
[dol~Principle(Loan)]
|
|
|
q2
|
I
|
[dol~Interest(Loan)]
|
q1*q3*q4
|
|
q3
|
|
[month~Time(Thing)]
|
|
|
q4
|
r
|
[dol~Interest(Loan)] /([dol~Principle(Loan)]*
[month~Time(Thing)])
|
|
|
q5
|
a
|
[dol~Amount(Loan)]
|
q1+q2
|
|
|
|
7.11
|
Dynamic Systems
|

|
|
|
|
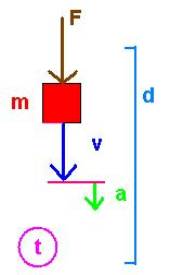
|
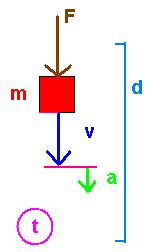
d [m~Distance(FallingThing)]
t [s~Time(FallingThing)]
v [m/s~Velocity(FallingThing)]
a [m/s2~Acceleration(FallingThing)]
m [kg~Mass(FallingThing)]
F [N~Force(FallingThing)]
|
A Dynamic System
|
The word "dynamic" implies that things are in
motion. Sir Isaac Newton, one of the
inventors of calculus, explored the relationships between the dimensions
associated with things attracted to each other by gravity. Today we use his name to specific a unit
of force; so 20 N (read twenty newtons) specifies an amount of force. By definition N=kg*m/s2. He found that the acceleration (a) that
pulls a thing toward the earth is a constant of proportionality between the
Force (F) exerted on the thing and the mass (m) of the thing. So for gravity, F=m*a. This and other relationships characterize
a dynamic system:
|
Qty
|
Value
|
Meaning
|
Relationship
|
|
q1
|
d
|
[m~Distance(FallingThing)]
|
|
|
q2
|
t
|
[s~Time(FallingThing)]
|
|
|
q3
|
|
[m/s~Velocity(FallingThing)]
|
q1/q2
|
|
q4
|
a
|
[m/s2~Acceleration(FallingThing)]
|
q3/q2
|
|
q5
|
m
|
[kg~Mass(FallingThing)]
|
|
|
q6
|
F
|
[N~Force(FallingThing)]
|
q5*q4
|
|
|
|
7.12
|
Activities and Explorations
|

|
|
|
|
|
Activities:
|
|
List relationships
Develop a list of relationships
from the explorations below.
Get Physical
Explore relationships in nature
(notice how many things are proportional)
http://www.walter-fendt.de/ph11e/
|
Explorations:
Exercises:
|
|
Do Related Problems In Your Textbook
|
|
|
Home
| Top
Copyright ©
2004 Dr. Ranel E. Erickson
|