Chapter 8.  Functions

The concept of a "function" permeates mathematics since it describes how one quantity (called the dependent quantity) depends on other quantities (called independent quantities).  We can use symbols and strings of characters (like "avg" above) to name a function; usually the generic letter f.  Similarly, variables can have various symbols and strings of characters to name them, usually the generic letter x.   The independent quantities appear in parenthesis immediately after the name.

Each expression placed in the Relationship (or Value Column) describes how that particular quantity depends on other quantities in the system of things.

Clearly defined meaning can have a great impact, especially when determining how one thing depends on another thing.  The mathematical statement above indicates that the quantity c depends ont the quantity  v.  If v has a value of 10, then c would have a value of 25.  After attaching meaning, we see that for any instance of mixed vegetables (the system of things), the function determines how two associated quantities "grow" with each other.  The more vegetables we have the more cost we incur.  The second line in this meaning table implies that the second quantity depends on the first quantity through the statements  c=f(x)=2.50*x

A quantity in the meaning table may depend on more than just one quantity as in the above example.  Here we have the perimeter dimension of a rectangle depending on both the height dimension and the width dimension.  The entry in the Relationship column establishes the functional relationship;  it shows how the quantity q3 depends on quantities q1 and q2, or in terms of the specific state symbols how p depends on w and h.

Similarly, dimensions and the functions that relate those dimensions can characterize a system of things.  In Unified Math®, we define a thing or a system of things not only by the dimensions that we measure, but by the way those dimensions depend on each other through two types of functions:  growth functions and horizon functions.

Similarly, if we double the size of a rectangle, we may expect an increase that preserves a constant ratio between the two sides. 

We can calculate the constant of proportionality c using any particular pair of quantities associated with a particular instance of the rectangle, namely c = q₂ / q₁ . 

All other quantities (perimeter, area, diagonal, etc.) that characterize this rectangle also belong to this particular state of the rectangle.  When solving word problems, we solve for values of the variables; and in doing so, we actually determine a particular state of a system having specific numeric values.  Usually we can have many quantities and relationships to our disposal when solving complex problems.  The challenge lies in identifying enough related quantities so that all quantities link back to known values.   The modeling process becomes like a game, looking for various jigsaw puzzle pieces to connect together into an abstract “picture” of the thing.

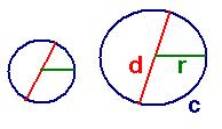
The growth functions (displayed explicitly in the Relationship column) of the abstract thing “Circle” show how the diameter, circumference, and area dimension of a circle "grow" as the radius dimension grows.  Notice that if we increase the size of a circle, then the growth functions determine how each of the other dimensions increases as r increases.  If we double the radius, then we double the diameter and the circumference.  These are examples of proportional growth functions.  The area dimension, though, grows faster than just proportional; it grows by the square of the increase.  If we triple the diameter, the area would increase by a factor of 3².

The rest of the sections of this chapter give a brief introduction to the two fundamental concepts in calculus to help you appreciate the far reaching impact that Unified Math® has in using meaning effectively.  You may skip these sections if you want to focus only on high school and first year college algebra concepts.

Chalk Board Example

To obtain a derivative function of a given function go to the site: http://www.quickmath.com/  and select the menu option "Calculus / Differentiate". 

To view the tangent line as you scan the function go to the webpagehttp://www-math.mit.edu/18.013A/tools/tools04.html

Chalk Board Example

To obtain an integral function of a given function go to the site: http://www.quickmath.com/  and select the menu option "Calculus / Integrate".

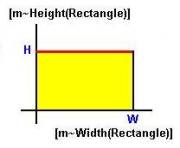
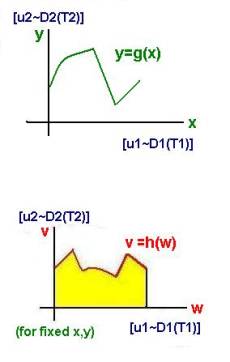
The horizon function h(x) determines how a dimension “shapes itself” around another dimension for each given state of a system of things.  For example, in the case of a specific instance of a rectangle (with fixed H and W), we can graph the shape of that instance.  Notice that this is not the growth function g(H)=W discussed earlier.  In the horizon function h(x), the height is a constant H over the interval from 0 to W along the width dimension of the rectangle.

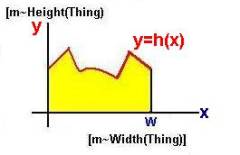
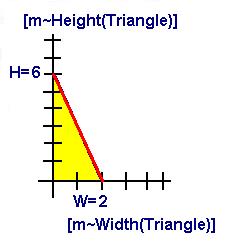
What is the height of this triangle?  Did you answer 6?  This indeed represents the traditional idea of the height of a triangle.  But 6 is the height only at the value 0 on the horizontal axis.  The height is actually determined at each point along the x axis by the horizon function f(x) = 6 – 2 * x  for 0 < x < 2.  This function depends on a particular state (where W = 2 and H = 6) of the right triangle with given growth function H = g(W) = 3 * W.  The general horizon function is  y=h(x) = H – W * x  for 0 < x < W. 

 The system of triangles defined by these growth and horizon functions consists of the set of all triangles similar to this one.  For any triangle in this system, we calculate the product of two scaled dimensions [m~Height(Triangle)] and [m~Width(Triangle)] with corresponding quantities H and W as the area underneath the above horizon function.  Using the concept of an integral from Calculus, we can express the area of each instance of a triangle in the system of triangles as a function of their maximum height H and maximum width W:

              ¥                  W                                                            W

              I   h(x) dx  =  I ( H – 3 x ) dx  =  ( H x – (1/2) 3 x² )    |    =  3/2 W² 

-¥                   0                                                               0

                                                            =   1/2 W * 3W  =  1/2 W * H 

The last expression in these string of equalities confirms to the traditional formula for the area of a triangle.  For the state of the system where W = 2 and H = 6, the “area” is 3/2 * 2² = 6. 

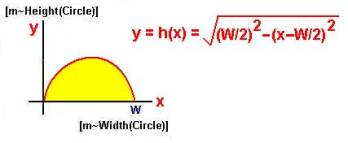
As another example, consider a circle with the x axis along the diameter of the circle:

The analysis applied to a triangle above applies to a circle as well.  The function though is a lot more complicated.  You many want to enter this expression into a calculator with a specific value of W, say 10 and see if the area under the curve (the integral from 1 to 10) gives the anticipated value of one half of the area of a circle with radius 5.

The multiplication of two generic scaled dimensions: [u2~D2(T2)] * [u1~D1(T1)] has the interpretation of “area” underneath the horizon function, that determines the shape of D2 over D1 for a particular instance of the things T2 and T1, in other words, for fixed x and y values.   The result gives us a growth function that relates the resulting dimension to D1 and D2.  Many of the results of such calculus computations have already become familiar grow functions to us including common area formulas for rectangle, circle, triangle, and trapezoid.  Many graphing calculators can give you the area under a curve.  They do so by applying the concept of an integral from calculus.

The division of two generic scaled dimensions: [u2~D2(T2)] / [u1~D1(T1)] has the interpretation of an instantaneous rate, the change of D2 per change in D1.  If we multiply the result by the scaled dimension [u1~D1(T1)]  in the denominator:

([u2~D2(T2)] / [u1~D1(T1)] )* [u1~D1(T1)]

and apply the definitions we see that the cancellation rule of Unified Math corresponds to the fundamental theorem of calculus:

I dg(x)/dx  dx    = g(x)

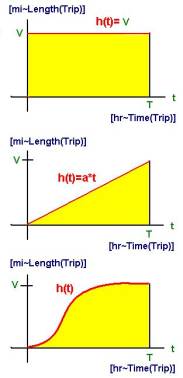
One usually encounters a "shock" when they try to apply their traditional methods of solving word problems to the concepts of speed.  Where does the ½ come from in the second equation above.  Many textbooks gloss over this by discussing it from the point of view of an average velocity.  In reality, the first formula is not a growth function to be applied in cases.  Instead, it and the second equation are special cases of the third equation.

First equation: D = I  h(w) dw  = I  V dw  =  V*w | ₀^T = V*T

Second equation:  D = I h(w) dw  = I a*w dw  =  ½*a*w² | ₀^T = ½*a*T² = ½*(a*T)*T = ½*V*T

You can apply these same concepts to the calculation of man-hours.  Go ahead and create a graph of man hours that is not the trivial rectangle and calculate the actual man hours as an area under the curve.

Geometry

[m2~Area] = [m~Width] * [m~Height]

[m2~Volume] = [m~Width] * [m~Height] * [m~Depth]

Mechanics (derived from meter, kilogram, second)

[m/s~Speed] = [m~Length] / [s~Time]

[meter/second2~Acceleration] = [m/s~Speed] / [s~Time]

[newton~Force] = [kilograms~Mass] * [meter/second2~Acceleration]

[joule~Energy = [newton~Force ]*[meter~Length]

[watt~Power] = [joule~Energy]/[sec~Time]

Electronics (derived from meter, kilogram, second, and amp)

      (Visualize a coulomb as the combined charge created by 1.6 x 10-18 electrons)

[amp~Current] = [coulomb~Charge] / [sec~Time]       

[volt~ElectromotiveForce] = [joule~Energy] / [coulomb~Charge]

[ohm~Resistance] = [volt~ ElectromotiveForce] / [amp~Current]

As illustrated above, we define most common dimensions by simple multiplications and divisions; and in doing so, set them up for use in meaning tables using the derivatives and integrals of the growth and horizon functions that characterize the system.

 Activities:

Explorations:

Exercises:

Home  |  Top

Copyright © 2004  Dr. Ranel E. Erickson