Chapter 12.  Definition Models

The fundamental operations of arithmetic (addition, subtraction, multiplication, and division) when applied to dimensions result in specific formulas as discussed in the previous chapter.   So the entry in the relationship column defines that operation.   In general, we consider an entry in the Relationship column as a way of defining dimensions in the Meaning Column.

For example the dimension "Average" invokes in our minds a formula, which in essence defines what we mean by "average".  This defining formula relates the quantity (with that meaning) to other quantities in the meaning table either previously defined or introduced further on in the table when the formula is introduced.  In this process, we focus our attention on the way that quantities relate to each other, and we formulate many small well-defined equations.  We suppress the desire to start solving these equations during the formulating process; this helps us to see the full model rather than just a glimpse of a particular state of the system.

Thus, the examples in this chapter often contain multiple equations containing multiple variables.  In later chapters, we will use algebra principles to solve such simultaneous equations.  For now (especially if you do not know how to solve such equations), just use a software application that solves systems of equation like the one at the site http://www.quickmath.com/ where you can select the menu option "Equation / Solve", and select the advanced version.  (See Chapter 15 for more information.)

Identify: 

When identifying quantities in the problem, also look in previous meaning expressions for scaled dimensions not yet been defined and enter them on their own line.  Quantities q6 and q7 come from q2 and q5 respectively. 

Relate: 

Quantities q2 and q5 have proportional meaning expressions so we can create the corresponding ratio of quantities in the relationship column implying that q2=q6/q1 and q5=q7/q1.  In order to relate the meaning [dol~Raised] to any other meaning, we realize that the definition of the dimension Raised involves the total cost of the items; hence a sum in the Relationship column on the third line. 

Formulate: 

q2=q6/q1

q3=q6+q7

q5=q7/q1

or more specifically for this state of the system:

5=q6/x

150=q6+q7

30=q7/4

Solve: 

q6=5*x  (from first equation)

q7=30*4=120  (from third equation)

150=5*x+120  (from second equation)

30=5*x

6=x

Source:  10 Real SATs, p. 145, The College Entrance Examination Board, New York

The first four quantities come from the word problem explicitly.  Notice that we only need to distinguish between two instances of a dimension like Time1 and Time2 if their values can differ.  In this situation, we do not need to distinguish between two different Length dimensions since this dimension is the same no matter what speed we use.  The next quantity provides a unit conversion between the two different units (minutes and hours) for the dimension "Longer".  The rest of the quantities finish documenting all the scaled dimensions used in the previous lines.

Obvious relationships come from the proportional meanings resulting in the divisions in the relationship column.  But a non-obvious relationship comes from the definition of the dimension "Longer".  This dimension invokes the generic dimension of difference, and in particular, the difference between Time2 and Time1 as indicated in the relationship column for q8.

Formulate: 

q2=q7/q3

q4=q7/q6

60=x/q8

q8=q6-q3

More specifically for this state we have:

70=q7/4

60=q7/q6

60=x/q8

q8=q6-4

Solve: 

q7=70*4=280  (from first equation)

q6=q7/60=280/60  (from second equation)

q8=280/60-4  (from fourth equation)

x=60*q8=60(280/60-4)=280-240=40

Formulate: 

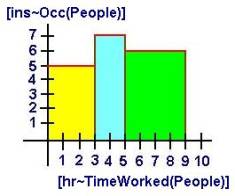
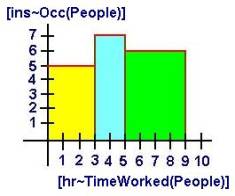
The information in the problem describes the horizon function that defines how the number of people working spreads out over the time dimension:

h(x) = 5 for 0<x<3

h(x) = 7 for 3<x<5

h(x) = 6 for 5<x<9

Solve: 

x  = I h(x)dx = 5*3+7*2+6*4 = 53

By definition, the dimension man-hours represents the multiplication of the two dimensions "number of men (and women) working" and "number of hours worked".  More formally, we could translate this into a meaning expression such as:

[ins~Occurrence(People)]*[hr~Time(People)]

The area underneath the horizon function gives the result of this multiplication of two dimensions.  In this particular case, the definition reduces to the sum of products of each time period where a constant number of people worked times the number of people that worked during that time period.

Formulate: 

(20/100)=q4/50

q4=x-50

Solve:

We show in detail how to solve simultaneous equations in Chapter 15.  Briefly, in the first equation solve for q4=10 and substitute this number into the second equation (10=x-50) and solve to get x=60

Alternative Approaches:

There often exists many ways to express the same algebraic relationships and thus many ways in which we might enter information into the meaning table.  The end result is still the same; we still end up with all the values for each quantity q1, q2, ... in the meaning table.  In this case, instead of entering the relationship of q2, q4, q3 in the second row (for q2) we could have put it in the last row (for q4).  When entering more than one relationship into a row, we use an equal sign to connect it to the other relationships in the row.  (Remember that everything across the row equal each other.)

Then we could have proceed just substituted the values for q1, q2, and q3 into the equation in the last row:

Formulate: 

x-50=(20/100)*50

Solve: 

x = (20/100)*50+50 = 10+50 = 60

Source:  10 Real SATs, p. 144, The College Entrance Examination Board, New York

The definition of average height implies that we divide the total of a group's height by the number of players in that group.  This definition gives us the quotient expressions in the Relationship column.

Formulate: 

x = q7 / 2

175 = q8 / 4

180 = q9 / 6 = (q7+q8) / 6

Solve:

q7 = 2*x

q8 = 175*4 = 700

180 = (q7+q8) / 6 = (2*x + 700) / 6

180*6 = 2*x + 700

1080 - 700 = 2*x

x = 380/2 = 190

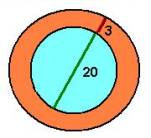
Source:  College Algebra, Sullivan, p 27

Formulate: 

A = q5-q6 = p*q9^2 - p*q8^2

P = p*2*q9

20 = 2*q8

3 = q9-q8

Solve: 

q8 = 20/2 = 10   (equation 3)

q9 = 3 + q8 = 13   (equation 4)

A = 3.1416*(169-100) = 216.7

P = 3.1416*2*13 = 81.68

Even though the problem only asks for two quantities,  the meaning table provides values to all the related quantities considered when finding the requested quantities.  In general, the meaning table provides way of documenting the measurements of a system of things.

Source:  REA Super Review Physics, p.313

Find the minimum radius for a planet of mean density 5,500 kg/m³  and temperature 400 degrees Celsius which has retained oxygen in its atmosphere.

Definition Relationships Used:

Formulate: 

General Model:

5500 = q4 / q5

q5=(4/3)*3.1416* r^3

673 = .032/(3*8.315)* q6^2

q6 = sqrt(2*6.67*10^-11* q4/r)

Again using the equation solving application at http://www.quickmath.com/  we have:

Notice that we not only get the radius of the planet but also its mass (q4), density (q5), and the escape velocity (q6)

Notes:

The presentation in the REA book is typical of physics texts.  It mixes the “relate” steps with the “solve” steps and drags the reader through a path of proof like steps.  The unified math approach uses the meaning table and the 5 steps of modeling as follows:

First we identify 3 quantities, the desired radius r and two numeric constants given in the problem.  Then we assign meaning to each of these quantities.

We relate Temperature to dimensions Mass and Length through formulas in the Kinetic Theory of Gases.  Of the many equations available in that theory we choose the one that involves velocity because of the phrase “retain oxygen”.  What does “retain oxygen” mean?  The average speed of Oxygen molecules would need to be just under the Escape velocity.  So a minimum radius would be such that the escape velocity equals the temperature velocity, namely,  v=sqrt(2GM/r)

Resource:  http://dbhs.wvusd.k12.ca.us/GasLaw/KMT-Gas-Laws.html

Build lists of key phrases associated with a given dimension.  For example the above list provides some alternative words and/or phrases to dimensions that imply basic algebraic operations.

 Activities:

Explorations:

Exercises:

Home  |  Top

Copyright © 2004  Dr. Ranel E. Erickson