|

|
How
to Solve Word Problems Programmatically
|
Chapter
13
|
|
|

|
|
|
|
Chapter 13. Simplifying Expressions
|
|
|
|
|
|
|
|
|
13.1
|
Substituting Numbers
|

|
|
|
Expression
|
Substitution
Numbers
|
Results
|
|
(a+b)*c
|
a=4, b=2, c=3
|
|
|
a*q2^q1
|
a=4, q1=2, q2=3
|
|
|
y/-x^2
|
y=8, x=2
|
|
|
third/first*second
|
first=2, second=3, third=12
|
|
|
a+b*c
|
a=4, b=2, c=3
|
|
|
q-r+s
|
q=6, r=2, s=3
|
|
|
a+b+c
|
a=2, b=4, c=5
|
|
|
5+4*x-3*x^2
|
x=2
|
|
|
a+x/b-x/c
|
a=4, b=2, c=3, x=6
|
|
|
3*(x+2)-x^2
|
x=-3
|
|
Substitute the numbers into their corresponding
expressions and calculate what you think is the value of the expression. Do not worry about right or wrong. The purpose of this exercise is to help
you become aware of the conventions that mathematics uses to evaluate
expressions.
Be aware that we use the sign "-" in two
different ways, as a "negative" sign and as a
"subtraction" operator. The
subtle difference between these two uses can cause problems if you do not
take care. One of the basic rules of
algebra (discussed later) defines subtraction as adding the additive inverse
(indicated by the negative sign) of a number: a-b=a+(-b).
|
|
|
13.2
|
Evaluating Numbers
|

|
|
|
Expression
|
Substitution
Numbers
|
Results
|
|
(a+b)*c
|
a=4, b=2, c=3
|
(4+2)*3=6*3=18
|
|
a*q2^q1
|
a=4, q1=2, q2=3
|
4*(3^2)=36 or
(4*3)^2=144
|
|
y/-x^2
|
y=8, x=2
|
8/-(2)^2=-2 or 8/(-2)^2=4
|
|
third/first*second
|
first=2, second=3, third=12
|
(12/2)*3=18 or 12/(2*3)=2
|
|
a+b*c
|
a=4, b=2, c=3
|
2+(4*3)=14 or (2+4)*3=18
|
|
q-r+s
|
q=6, r=2, s=3
|
(6-2)+3=7 or 6-(2+3)= 1
|
|
a+b+c
|
a=2, b=4, c=5
|
(2+4)+5 = 2+(4+5)=11
|
|
5+4*x-3*x^2
|
x=2
|
multiple possibilities
|
|
a+x/b-x/c
|
a=4, b=2, c=3, x=6
|
multiple possibilities
|
|
3*(x+2)-x^2
|
x=-3
|
multiple possibilities
|
Some of these examples have more that one result that seem
reasonable. Shall we vote on them
democratically? Mathematics resolves
this by a set of conventions (the language syntax) one of which specifies the
"order of operations". Try
putting these examples into your calculator and make sure you know the proper
keystrokes to get right answer as determined by the following order of
operations.
|
|
|
13.3
|
Order of Operations
|

|
|
|
Sign
|
Operations
|
Examples:
|
|
|
( )
|
paranthesis
|
(a+b)*c
|
(4+2)*3=6*3=18
|
|
^
|
exponent
|
a*q2^q1
|
4*3^2=36, not (4*3)^2=144
|
|
-
|
negative
|
y/-x^2
|
8/-(2)^2=-4, not 8/(-2)^2=4
|
|
/
|
division
|
third/first*second
|
12/2*3=18, not
12/(2*3)=2
|
|
*
|
multiplication
|
a+b*c
|
2+4*3=14, not (2+4)*3=18
|
|
-
|
subtraction
|
q-r+s
|
6-2+3=7, not 6-(2+3)= 1
|
|
+
|
addition
|
a+b+c
|
(2+4)+5 = 2+(4+5)
|
The order in which these operations appear in this table,
determines which of these operators we do first. Parenthesis always goes first; so when you want an expression
to calculate first, put it in parenthesis.
|
Traditional notation used in textbooks sometimes hides
operations (especially multiplication, exponentiation and
parenthesis). By converting
traditional notation to a text-string notation used by many computer
software applications, we see explicit symbols for each operation and can
determine more readily the sequence of operations calculated.
|
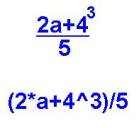
|
These rules establish the conventions upon which we read a
mathematical statement. As
demonstrated by the examples, understanding which operation we do first can
make or break an effort to solve a word problem. Now even the most complicated expressions end up with only one
accepted value:
|
Expression
|
Substitution
Numbers
|
Results
|
|
5+4*x-3*x^2
|
x=2
|
5+4*x-3*x^2=5+8-12=1
|
|
a+x/b-x/c
|
a=4, b=2, c=3, x=6
|
4+6/2-6/3=4+3-1=6
|
|
3*(x+2)-x^2
|
x=-3
|
3*(-3+2)-(-3)^2=-3-9=-12
|
|
|
|
13.4
|
Basic Algebra Rules
|

|
|
|
Rule Name
|
Statement
|
Example
|
Simplify:
|
|
(Addition)
|
|
|
|
|
Identity
|
a+0=a
|
2/3+3/2-6/4
|
|
|
Inverse
|
a+(-a)=0
|
5+(1-6)
|
|
|
Commutative
|
a+b=b+a
|
-4+5/2+4
|
|
|
Associative
|
(a+b)+c=a+(b+c)
|
(5+-6)+6
|
|
|
Definition of Subtraction
|
a-b=a+(-b)
|
4-(-6)
|
|
|
|
|
|
|
|
(Multiplication)
|
|
|
|
|
Identity
|
a*1 = a
|
(4-8/4)*(3-2)
|
|
|
Inverse
|
a*(1/a)=1
|
6*8*(1/6)
|
|
|
Commutative
|
a*b=b*a
|
5*9/5
|
|
|
Associative
|
(a*b)*c=a*(b*c)
|
(3*4/5)*5
|
|
|
Definition of Division
|
a/b=a*(1/b)
|
4/(1/4)
|
|
|
|
|
|
|
|
(Connects Them)
|
|
|
|
|
Distributive
|
c*(a+b)=c*a+c*b
|
12(3/4+5/12)
|
|
These 11 rules form the
foundation for algebra. Just like
geometry can be constructed from just 5 rules (Euclid's postulates), most of
algebra can be derived from the above rules.
Go ahead and simplify each of the above examples to illustrate the
corresponding rule (and sometimes use some of the other rules.)
|
|
|
13.5
|
Using Rules to Simplify Expressions
|

|
|
|
Rule
|
Statement
|
Example
|
Results:
|
|
(Addition)
|
|
|
|
|
Identity
|
a+0=a
|
3/4+3/2-6/4
|
3/4
|
|
Inverse
|
a+(-a)=0
|
5+(1-6)
|
0
|
|
Commutative
|
a+b=b+a
|
-4+5/2+4
|
5/2
|
|
Associative
|
(a+b)+c=a+(b+c)
|
(5+-6)+6
|
5
|
|
Definition of Subtraction
|
a-b=a+(-b)
|
4-(-6)
|
10
|
|
|
|
|
|
|
(Multiplication)
|
|
|
|
|
Identity
|
a*1 = a
|
(4-8/4)*(3-2)
|
2
|
|
Inverse
|
a*(1/a)=1
|
8*6*(1/6)
|
8
|
|
Commutative
|
a*b=b*a
|
5*9*(1/5)
|
9
|
|
Associative
|
(a*b)*c=a*(b*c)
|
(3*4/5)*5
|
12
|
|
Definition of Division
|
a/b=a*(1/b)
|
5*9/5
|
9
|
|
|
|
|
|
|
(Connects Them)
|
|
|
|
|
Distributive
|
c*(a+b)=c*a+c*b
|
12(3/4+5/12)
|
14
|
Did you get these results when
you evaluated these expressions?
These rules allow us to simply expressions with variables just as
easily as we evaluated these expressions.
To illustrate this, go ahead and use these basic rules to simplify the
following expressions.
|
Example
|
Results:
|
|
|
|
|
3/4+6*x/2-3*x
|
|
|
5+(x-6*x)*(1/x)
|
|
|
-4*x+5*x^2/2+4*x
|
|
|
(5*x^2+-6*x)+6*x
|
|
|
4*x-(-6*x)
|
|
|
|
|
|
(4*x-2)*(3*x+1-3*x)
|
|
|
8*x*(6+x)*(1/(6+x))
|
|
|
5*x^3*9*(1/(5*x^3))
|
|
|
(3*x*4/5)*5
|
|
|
5*x^3*9/(5*x^3)
|
|
|
|
|
|
12(3*x/4+5*x/12)
|
|
|
|
|
|
Rule
|
Example
|
Results:
|
|
(Addition)
|
|
|
|
Identity
|
3/4+6*x/2-3*x
|
3/4
|
|
Inverse
|
5+(x-6*x)*(1/x)
|
0
|
|
Commutative
|
-4*x+5*x^2/2+4*x
|
5*x^2/2
|
|
Associative
|
(5*x^2+-6*x)+6*x
|
5*x^2
|
|
Definition of Subtraction
|
4*x-(-6*x)
|
10*x
|
|
(Multiplication)
|
|
|
|
Identity
|
(4*x-2)*(3*x+1-3*x)
|
4*x-2
|
|
Inverse
|
8*x*(6+x)*(1/(6+x))
|
8*x
|
|
Commutative
|
5*x^3*9*(1/(5*x^3))
|
9
|
|
Associative
|
(3*x*4/5)*5
|
12*x
|
|
Definition of Division
|
5*x^3*9/(5*x^3)
|
9
|
|
|
|
|
|
Distributive
|
12(3*x/4+5*x/12)
|
14*x
|
|
|
|
|
|
|
|
13.6
|
Deriving Other Rules
|

|
|
|
|
(a+b)^2=a^2+2*a*b+b^2
or
equivalently
(a+b)2=a2+2*a*b+b2
|
Sum-Squared Rule
|
One nice feature of mathematics comes from the fact that
if you cannot remember a formula (like this expansion formula), you can often
remember related formulas and derive the forgotten one. The 11 basic rules presented above form
the foundation upon which we derive most of the other algebra rules. Let us use them to derive (prove) the
above sum-squared rule.
|
Rule
|
Reason
|
|
(a+b)^2=
|
|
|
(a+b)*(a+b)=
|
Definition of exponent
|
|
(a+b)*a+(a+b)*b=
|
Distributive rule (from left)
|
|
a*a+b*a+(a+b)*b=
|
Distributive rule on left multiplication
|
|
a*a+b*a+a*b+b*b=
|
Distributive rule on right multiplication
|
|
a*a+a*b+a*b+b*b=
|
Commutative rule on second term
|
|
a*a+2*a*b +b*b=
|
Associative rule on two middle terms
|
|
a^2+2*a*b +b^2
|
Definition of exponent
|
|
|
|
13.7
|
Rules for Factoring
|

|
|
|
Rule
|
Example
|
Result:
|
|
(a+b)2=a2+2*a*b+b2
|
(5+x)^2
|
|
|
(a-b)2=a2-2*a*b+b2
|
(1-x)^2
|
|
|
a2-b2=(a+b)*(a-b)
|
1-x^2
|
|
|
(a*x+b)(c*x+d)=a*c*x2+(a*d+b*c)*x+b*d
|
(2*x-3)*(5*x+4)
|
|
|
|
|
|
|
|
|
|
The last rule generalizes the factoring of a quadratic
expression. We often use it in
reverse where we have the expression on the right of the equal sign and then
determine the left side of the equation.
These techniques (usually covered in a second year algebra course)
take some practice, but are helpful in simplifying fractions of expressions
like the last added example. The
website http://icm.mcs.kent.edu/research/facdemo.html
allows you to enter a polynomial and get factors, if they exist. Try entering 10*x^2-7*x-12 and see what you
get.
Did you get the following results for the above table of
examples?
|
Example
|
Results:
|
|
|
|
|
(5+x)^2
|
25+5*x+x^2
|
|
(1-x)^2
|
1-2*x+x^2
|
|
1-x^2
|
(1+x)(1-x)
|
|
(2*x-3)*(5*x+4)
|
10*x^2-7*x-12
|
|
(10*x^2-7*x-12)/ (2*x-3)
|
(5*x+4)
|
|
|
|
http://www-math.mit.edu/18.013A/tools/tools04.html (Visual blocks to represent factors)
|
|
|
13.8
|
Rules for Fractions
|

|
|
|
Rule
|
Example
|
Result:
|
|
(a/b)*b=a
|
((x+7)/4)*4
|
|
|
a/b+c/d=(a*d+c*b)/b*d
|
x/2+y/6
|
|
|
a/b-c/d=(a*d-c*b)/b*d
|
1/3-2/A
|
|
|
(a/b)*(c/d)=(a*c)/(b*d)
|
(((x-5)^2)/5)*(5/(x-5))
|
|
|
(a/b)/(c/d)=(a/b)*(d/c)
|
(4/c)/(c/2)
|
|
|
(a/b)^n = a^n / b^n
|
(x/3)^n
|
|
Discussion of
fraction rules can be found at
http://library.thinkquest.org/20991/textonly/alg/frac.html
|
|
|
13.9
|
Rules for Exponents
|

|
|
|
Rule
|
Example
|
Simplify:
|
|
ax*ay=ax+y
|
(2+y)5(2+y)-4
|
|
|
(ax)y=ax*y
|
((2 (1/x+1))2*x
|
|
|
(a*b)x=ax*bx
|
(1+x)3 * (2/(1+x))3
|
|
|
ax/ay=ax-y
|
z5/z3
|
|
|
a-x=1/ax
|
(2+y)4*(1/(2+y) 3)
|
|
|
(a/b)x
= ax/bx
|
(1-x2)3/(1-x)3
|
|
|
|
|
13.10
|
Activities and Explorations
|

|
|
|
|
|
Activities:
Explorations:
Exercises:
|
|
Do Related Problems In Your Textbook
|
|
|
Home
| Top
Copyright ©
2004 Dr. Ranel E. Erickson
|