Chapter 14.  Solving For Variables

The balance principle is the "golden rule" of algebra:  Do unto one side as you do unto the other.  In general, we can view this rule as applying the same function to both sides of an equation.  In its simplest form, the functions just apply a particular operation with a given quantity.  In the first example above, we just add 3 to both sides of the equation.  Similarly, for the next three examples we simply subtract, multiply, or divide both sides of the equation with the same quantity. 

The next two examples show demonstrate the use of the square function and its opposite the square root function.  These functions represent inverse functions of each other.  Similarly the power of 10 is the inverse function of the log base 10 function and the natural log function f(x)=ln(x) provides an inverse for the (natural) exponential function f(x)=exp(x). 

In order to isolate the variable in each of the examples above, we applied the inverse of the operation we want to reverse.  The first equation involved a subtraction so we added, the third one a division so we multiplied, etc.  This works fine if we have only one operation.  But what do we do when there exists more than one operation in the expression.  Let us consider several effective strategies.

If we have an equation with a single symbol to isolate, then we can follow a strategy of reversing the order of operations as we untangle it from its surrounding computations.  This example has one occurrence of one variable x.  It appears in the equation with two operations surrounding it, a multiplication "*" and a plus "+".  The multiplication operation would occur before the plus operation.  So to isolate x we reverse this order and use an inverse function of the plus operation to "peel" off the 6, then we use a inverse function for the multiplication operator to "peel" off the 4.

Now that you are warmed up, try this one.  It has three operations and one set of parenthesis.

The operations on the same side of the equation as the x would occur in the following order: the subtraction "-" surrounded by parenthesis, then division "/", and then addition "+".  So in reversing this order we would subtract 2 from both sides.  Proceeding we have:

Notice that when the variable x would switch from one side of the equation to the other, we still kept our focus on isolating that variable and continued to peel off operations surrounding it.

When there exists more than one occurrence of the variable in the equation, then we need to combine terms.  In a polynomial, each term consists of a constant times the variable raised to a particular power.  The expressions 2*x^2, 4*x, and 3 are terms that appear in the above example.  When solving equations that have polynomial terms in them, we seek to combine all terms of the same power together; so we repeatedly apply the balance principle and simplification rules to achieve this goal.  In the example above, we first simplify by expanding the power of the sum (1+x) in order to achieve individual terms. Then we combine terms and move all terms over to the left side of the equation to create a polynomial expression.

Several of the powered terms in this example canceled out allowing us to solve this problem using strategies discussed previously.  If other powered terms remain, the problem becomes much more difficult to solve.  We can, though, determine a solution set for polynomials containing terms up to the second power.  Such polynomials are called quadratic equations.  As an example consider solving the following equation for x.

This final polynomial has more than one power term so we cannot continue to isolate a single x.  What we can do, though is use the quadratic formula, since this is a quadratic equation (a polynomial of degree 2).

The quadratic formula can provide 0, 1, or 2 solutions.  No solution occurs if the discriminant b^2-4*a*c is less than 0, because a negative value inside the square root function does not make sense in the real number system.  If the discriminant has a value of 0 then we have 1 solution, namely, -b/2*a.  Otherwise we have the two solutions as indicated above.  Example:

In this example, a=1, b=1, and c=-12.  The points x=3 and x=-4 satisfy the original equation.

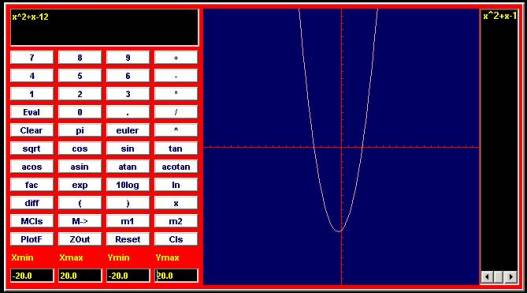
f(x)=x^2+x-12=0 

crosses x-axis at x=-4 and x=3

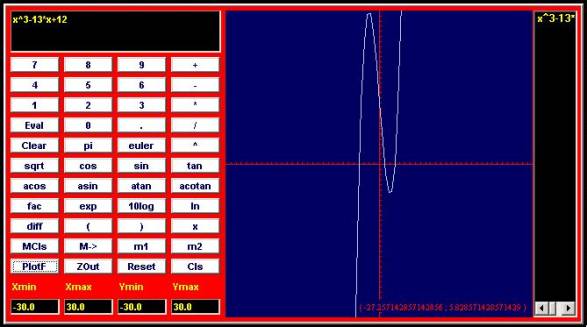
The solutions provided in the quadratic formula can have a visual representation as numbers on the x-coordinate where the function crosses over the x-axis.  In this case, the quadratic curve crosses the x-axis at x=-4 and x=3.  We call such points on the x-axis where the function equals 0 the roots of the function.  The following example shows that a cubic function can have 3 roots.  In general, a polynomial function of n-th degree can have up to n roots; therefore, when we solve for the variable x in such a polynomial, we can find up to n values that satisfy the equations.

f(x)=x^3-13*x+12=0 

crosses x-axis at x=-4, x=1, and x=3

Computer software that solves such problems use techniques that find roots of the general equation f(x)=0 efficiently.

Sometimes the original equation has expressions involving the variable that we want to isolate in the denominator.  In such a case, multiply by such expressions to move them up into the numerator.  In this example, we multiply by (1-2*x) to remedy this situation.  Then we can proceed as before, combine terms and find roots.

In addition to polynomials, similar strategies hold for functions in general.  The goal still encourages us to isolate the x value.  In this case we combine like terms that involve ln(x) and then apply the inverse function f(x)=exp(x) to find a solution.

This example has two different variables (q1 and q2) but only one occurrence of the variable q2 that we desire to isolate.  So we can use an strategy similar to the Example I above.  Now that you are warmed up, let us try a challenging one that involves 5 operations.

Do not panic!  Just start reversing operations that surround the variable at any given stage of the isolation process. 

Even though we might end up with a complicated expression (or in this case two expressions), we have isolated the variable y and have determined solutions to the original equation.  As an exercise in simplification, go ahead a substitute either one of the values of y back into the original equation and simplify.

 Activities:

Explorations:

Exercises:

Home  |  Top

Copyright © 2004  Dr. Ranel E. Erickson