Chapter 15.  Simultaneous Equations

Source:  College Algebra, Sullivan, p 532, p.21

The variables in a meaning table consists of the quantity symbols q1, q2, q3, etc. and any symbol introduced in the Value column.  When entering this meaning table, we gave our own variable names to quantities q1, q2, and q3 rather than just use the symbols q1, q2, and q3 to emphasize what we are looking for.  This is not necessary, but often done for reference convenience.  Notice that we did not give the last 3 quantities an alternative variable symbol. 

(We have purposely left out relationships associated with quantities q8 and q9 to illustrate what happens when we do not have enough equations.)

This problem was selected to illustrate the type of problems that occur at the college level and demonstrate your ability to solve complex problems by breaking up the problem into simple steps using the concepts discussed in this book.

The first entry in the Relationship column (associated with q4) comes from the definition of total.  The next three come from the division operator in the meaning columns assuming a price proportional to the number of seats purchased (no discounts for volume purchases).  Since each entry in the Value, Quantity, or Relationship columns in a row equal each other, we can have an equation between each entry and the corresponding quantity q1, q2, etc.  Listed in the order of appearance down each column we have:

a=q1, b=q2, c=q3,

500=q4, 50=q5, 35=q6, 25=q7

17100=q8, 14600=q9

q4 = q1 + q2 + q3

q5 = q10 / q1

q6 = q11 / q2

q7 = q12 / q3

The first nine equations (listed across the first three rows above) give us simple equations that assign values (either constants or assigned variable expression) in the Value column to the generic quantity variables (q1, q2, etc.).  So when we formulate the equations, we often immediately substitute such quantities into the other equations to get a formulation like:

17100=q8

14600=q9

500 = a + b + c

50 = q10 / a

35 = q11 / b

25 = q12 / c

We did not substitute q8 or q9 into any other equation, since no equations (in the current table) related them to the other quantities.

This system of equations contains 8 variables (a, b, c, q8, q9, q10, q11, q12) each of which we desire a value so that they satisfy all equations simultaneously.  Usually, it takes the same number of equations as variables for us to find a solution.  Since we have only 6 equations we need 2 more equations. 

Source:  College Algebra, Sullivan, p 532, p.21

When looking for additional equations, we ask ourselves how do the remaining quantities relate to each other.  After reviewing the problem again, we discover other relationships; we see that the words associated with 17,100 and 14,600 provide us with two more equations that relate the q8 and q9 quantities to the other three generic quantities:

17,100 = q10+q11+q12

14,600 = q10+q11+.5*q12

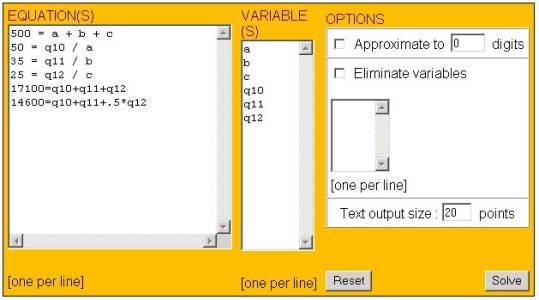
To solve this system of equations using the menu option "Equation / Solve (Advanced)" at the website http://www.quickmath.com/  we would enter the equations in the following input screen and get the subsequent results.  (Do not enter the commas)

This indicates that an approximate solution to our problem is a=106, b=193, and c=200, where we round down to obtain an integer number of seats.

How would we solve this without a computer?

We can solve some systems of equations (having same number of variables as equations) by repeatedly isolating a variable in a selected equation and substituting it into the other equations.  On dropping that equation, we have one less variable and one less equation.  You can select any equation and variable to isolate, but it often helps to begin by selecting a generic variable that is easy to isolate to simplify the amount of work that we have to do.  In this case quantity q10 (like q11 and q12) isolate easily. 

On isolating q10 we get, q10=50*a.  Likewise, we can also do this for quantities q11=35*b and q12=25*c.  The next step involves substituting these solved expressions for each appearance of these quantities in the other equations.  This results in a system of equations with 3 equations and three unknowns. 

We repeat this process for each of the other variables.  Let us continue by isolating the variable "a" in the first equation, primarily because it appears less complicated than in the other equations.  We now remove the equation that we solved, and simplify the resulting second and third equations.

17100=25000-50*b-50*c+35*b+25*c

15*b+25*c=7900

Go ahead and verify the other simplification:

Now solve for c in the first equation (because it isolates easier since 25 divides 7900 evenly) and substitute the results into the second equation:

Now we isolate the variable b:

15*b+11850-22.5*b=10400

7.5*b=1450

b=193.33

We substitute this value back into the other isolation equations to determine other values:

Now you can see why computers are so useful.  This process was tedious, but not "difficult" in the sense of being creative.  Indeed, the creative part of solving word problems is the stage in which we determine meaning; a computer can do the rest using programmable steps.

In some cases, it may appears as if we have the same number of equations as the number of variables; but two or more equations may actually represent the same relationship, just rearranged like illustrated above.  We call such equations "redundant ".  When we discover redundant equations (even in the process of solving the equations), we can remove them from consideration.  So, in this case, only one of these would count toward the number of statements in our system of equations.

 Activities:

Explorations:

Exercises:

Home  |  Top

Copyright © 2004  Dr. Ranel E. Erickson