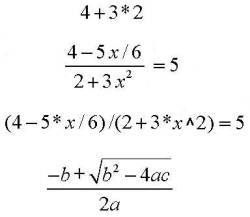Chapter 1.  Meaning

When studying a language you learn new words that identify and relate objects; such words form the foundation of that language.  Vocabulary words arise not only from different national, cultural, and ethnic backgrounds but from the different disciplines of knowledge such as medicine, business, construction, engineering, and biology, to name a few.

We can view mathematics as a language with its own set of vocabulary words and grammar rules that measure and relate things in the world around us.  A baby learns to speak a language naturally by experiencing the language in action.  This book uses a similar strategy by immersing you in the applications of mathematics using a systematic approach to solving problems that involve measurable quantities.  You will gain mathematical knowledge by naming, observing, and finding relationships between things and their properties (or dimensions).  Math enables us to record measurements, define abstract relationships and calculate results. 

When learning a new language, you often find yourself in a cyclic learning process where you continually encounter new words (or symbols), some of which you cannot completely comprehend, until you have learned other words, ideas, and concepts.   As your vocabulary grows, the ideas discussed earlier finally start to make sense.   For example, when learning a computer programming language, one seldom understands all the words and concepts the first time through a book.  You many need to cycle back several times before understanding all the vocabulary words.  This also applies to mathematics. 

As you begin to learn how to solve word problems programmatically, you may feel like trying to learn how to swim after falling into the middle of a lake.  Don't just turn purple with panic; start paddling vigorously through vocabulary at websites such as http://www.purplemath.com/modules/index.htm and the other exploration paths listed at the end of this chapter.  Remember, you gain vocabulary words through exposure.

Mathematics has its own grammar that can impact the way we read a mathematical statement.  The first example above can easily be mistakenly read 4+3 equals 7 times 2 equals 14.   But this translation does not follow the grammatical rules involving a hierarchy of operations (which we will discuss later).  These rules cause the multiplication operation to occur before the addition operation resulting in the translation 3*2 equals 6 plus 4 equals 10.

Furthermore, there exists different ways of expressing mathematical statements in printed form.  For example, the second and third examples above express the same mathematical statement.  The third example uses explicit symbols to represent each operation and function.  This approach is commonly used in computer applications.  Try rewriting the last expression using such explicit notation.

How does a noun like “city” relate to a proper noun like “Denver”?   Denver represents a specific value of the noun “city”.  When we make a statement like “A city has people in it,” we have created a general rule that remains true for the set containing all cities.  The city can vary; we can consider Denver, Los Angeles, Dallas, Paris, etc.  In particular, we can substitute the city “Denver” into the sentence and obtain the statement: “Denver has people in it.”  Notice how this statement remains true for every city name that we substitute. 

Similarly, in mathematics, variables correspond to nouns and numbers correspond to proper nouns.  We substitute numbers into variables to verify the statement.  If a statement holds true for a set of numbers then we say that the statement is a rule over that set of numbers.

A second use of variables expresses criteria (as opposed to rules).   Consider the sentence,  “The capital of the United States of America is a city.”  We interpret this not as a general statement but rather as specific criteria for a particular solution to satisfy.  On substituting “San Diego” into this sentance we get a false statement.  Whereas, the solution “Washington, D.C.” makes the statement true.  Similarly, when we create mathematical expressions from the words of a word problem, we formulate criteria that the solutions must satisfy.   In general, we use rule statements to manipulate criteria statements when solving for solutions of a word problem.

In general, a mathematical model for a word problem contains math criteria statements that represent the way numbers and variables relate to each other for a given system of things.  It allows us to calculate solutions to questions about the system.  For the previous word problem, we traditionally use the mathematical model "p*a=c" to relate the quantities in a system of items for sale where the quantity “c” represents cost, “p” represents price (of each item), and “a” represents the amount purchased.

When we assign specific numbers to selected variables in a model, it often determines the value of other variables as well.  These numbers correspond to a particular purchase.  The next purchase could have different numbers but those new numbers would also need to satisfy the criteria statement.  We identify a specific state of the system (or model) by assigning numbers to the variables.  In this example, a state of the general price model is determined by letting p=2 and c=12.  From these values we can solve for "a" and get a = 6. 

When building mathematical models we need to be careful when translating English statements into math statements.  Many people translate this phrase incorrectly.  If you answered “2*C=D”; then, like many other thrashing swimmers, you fell into one of the common traps when assigning meaning to quantities.  

How would this new programmatic method help?  In this translation the number 2 has the (abbreviated) meaning "cats/dog" (read "cats per dog").  So (as we will discuss in the next chapter) we multiply numbers with their meanings  "(2 cats/dog) * (D dogs) to cancel the dog unit result in an expression "2*D cats" that has the same unit as "C cats".  Hence  "2 * D cats = C cats".

Which of the above statements ring true.  Does 3=1?   This is not a trick question.  NO is the answer.  Do units (feet and yard) make the second statement "3 feet = 1 yard true?  At first, you may say YES; but by doing so you assumed that we are measuring the same dimension.  The third statement involves two different dimensions (length and width), so "3 ft length" and  "1 yd of width" do not measure the same dimension.    And even the same dimension may not be sufficiently clear, like "length" in the fourth statement, it also needs to be associated with the same thingin order to be exactly "equal". 

This book introduces a programmatic way of solving word problems using meaning.  In general, the book introduces you to a new kind of mathematics, which we call Unified Math.  Unified Math algebraically unifies quantities with their meaning.  To this end, we now define the three components of meaning:  unit, dimension, and thing.  As you will see, we need all three of these components to clearly define the mathematical models associated with word problems.

In order to assign meaning to quantities, we combine all three components of meaning (unit, dimension, and thing) into a scaled dimensionusing the general notation: [unit~Dimension(Thing)].

Unified Math introduces a new unit called "instance" and a dimension called "occurrence" to handle the "counting" of things.  Since "balls" actually is a "thing", we use "instance" as the formal unit.  Informally, we often use "ball" as if it were a unit; but from now on, recognize that the actual unit is "instance" and that the use of the word "ball" represents an abbreviation of "[instance~Occurrence(Ball)]:.   As you will see, this allows us to resolve the dilemma of "adding apples and oranges" when one of the rules in Unified Math requires that the units must be the same.

In addition to a single scaled dimension to provide meaning for quantities, we also use multiplications and divisions of scaled dimensions to create meaning expressions.   We call the combination of a quantity and its meaning expression a unified quantity.   Each entry above gives an example of a unified quantity attached to a numeric quantity.  In general, a quantity can be a number, a variable, or a mathematical expression of numbers and variables, and we can assign meaning expressions to such quantity expressions.

When solving word problems, we often use abbreviations.  But the three components of meaning should always be clear from the context without any chance of confusion.  The most common abbreviations of meaning consist of just the unit or just the thing.

We will use this meaning table to document our thought processes when formulating and solving mathematical models for quantitative problems.   This systematic approach enables us to solve word problems effectively.  It encourages us to define system quantities carefully before constructing their relationships, and to construct relationships before solving equations.

A word problem may ask for one or more quantities.  The meaning table calculates values for all the related quantities considered when finding the requested quantities. 

In general, the meaning table provides a way of documenting many of the measurements and relationships in a system of things.  It provides a systematic interface between raw data and models built upon on that data.  It opens up the opportunity to create a paradigm shift in the way we teach science.  It can allow us to document many quantities associated with a given system of things and emphasize all known relationships without excluding those that may not fit the current theories.  Theories often only provide "current" interpretations of "subsets" of the available data and relationships.

Take for instance a current popular theory of the universe, the "big bang" theory.  Most science textbooks discuss this theory leaving out data that suggests a relationship between increased distance and increased acceleration.   But this relationship goes against our expectation of objects on the outside of an "explosion" to slow down not accelerate.  History has proven that great discoveries have often occurred when people (like Galileo, Newton, Einstein, etc.) have pondered all quantities and quantity relationships especially those that did the not fit the current "beliefs" (or models) built on partial data.

What object does these unified quantities refer to?  Notice the use of abstract mathematical vocabulary, even when describing things associated with the object.  All of these things make up a quantitative system that describes the object.  This is an example of how to play the game "A World With Only Math".   Indeed, math helps us to describe more precisely the world around us.  Here is another example of how increased math vocabulary helps you to give more informative clues. 

Word problems provide information about quantities.  In general, we first identify the quantities that we seek and then find related quantities.  The above word problem asks for the time it will take for a car to travel a certain distance, so the first entry in the meaning table contains a variable "x" with a meaning that describes the desired quantity.  We then list the rest of the quantities in the order in which they appear in the problem.  Go ahead and identify the quantities and a meaning in each of the following word problems and then compare your results with the suggestions that follow.  Remember that your meaning expressions may use different words or different abbreviations; that is all right, just remain consistent.

You could also have abbreviated as follows since each unit explicitly determines the dimension and there exists only one thing in this problem.

This problem contains quantities whose meaning we cannot determine with units only.  We need to distinguish between the miles associated with the odometer and the miles actually driven.

 Activities:

Explorations:

Exercises:

Home  |  Top

Copyright © 2004  Dr. Ranel E. Erickson