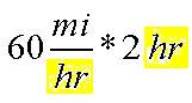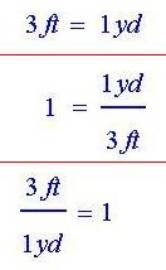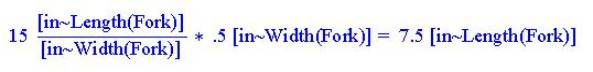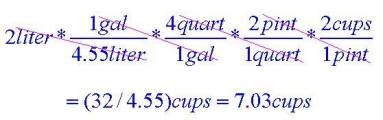|

|
How
to Solve Word Problems Programmatically
|
Chapter
2
|
|
|

|
|
|
|
Chapter 2. Extending Unit Analysis
|
|
|
|
|
|
|
|
|
2.1
|
Unit as a Meaning
|

|
|
|
|
|
This instance of a metal bar
has a length dimension whose quantity corresponds to either 3 in or 7.62
cm.
|
A unit specifies an amount of a given dimension. For example, there exists a metal bar
stored in France that the metric system used to represent the standard size
for a meter of length. Units provide
the basic building blocks of measurement.
The above measuring tape has two unit scales on it, one for inches
(in) and one for centimeters (cm). We
use multiples of a unit to measure other instances of an object. The 3-inch bar measured above is 3 times
as large as a metal bar that corresponds to one inch (a unit inch).
|
In general, a unit of a given dimension D of a given
thing T represents a quantity 1 of the dimension D for a specific
occurrence of the thing T. Each
other quantity q corresponds to an occurrence of that thing that is q times
as much.
If we measure the same occurrence of a thing using two different units then
the resulting unified quantities are equal.
|
q [u~D(T)]
3 [in~Length(Bar)] =
7.62 [cm~Length(Bar)]
3 in = 7.62 cm
|
|
1 in = 2.54 cm
1 [in~Dimension(Thing)]
= 2.54 [cm~ Dimension(Thing)]
16 oz = 1 lb
16
[oz~Dimension(Thing)] = 1 [lb~ Dimension(Thing)]
|
Equal
Unified Quantities
|
When we abbreviate and only mention units in unified
quantities and equations, we assume that the units measure their
corresponding default dimensions of a common thing.
|
|
|
2.2
|
Unit Identity
|

|
|
|
|
We frequently encounter equations used to express unit
conversions such as "3 ft = 1 yd".
If we divide a unit conversion equation like "3 ft
=1 yd" with the left-hand-side expression "3 ft" we obtain
the equation "1 = 1 yd / 3 ft".
Similarly, if we divide that same unit conversion
equation "3 ft = 1 yd" with the right-hand-side expression
"1 yd" we obtain the equation "3 ft / 1 yd = 1".
These new statements imply that both the expressions
"3 ft / 1 yd" and its inverse "1 yd / 3 ft" are unit
identity expressions that we can use as factors to multiply other unified
quantities without changing the actual amount of that dimension.
|
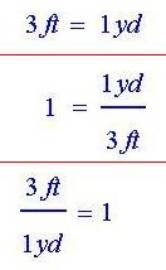
|
We can also express "3 ft / 1 yd" as "3
ft/yd" (read "3 feet per yard") and "1 yd / 3 ft" as
".33 yd/ft". Each of these
four expressions provides examples of unit identities. Some unit identifies result from
approximations such as "1 in ≈ 2.54 cm" or the result of
round off error such as "1/3=.33".
In these situations, we will still use the equal sign with an
understanding that it really means "nearly equal to".
|
1 in = 2.54 cm
|
2.54 cm/in
|
.394 in/cm
|
|
1 min = 60 s
|
60 s/min
|
.0167 min/s
|
|
1 gal = 4 pt
|
|
|
|
1 lb = 16 oz
|
|
|
|
1 kg = 1000 g
|
|
|
|
Fill in the unit identity
factors
|
Go ahead and fill in the blanks. See Unit Conversions
Appendix for more examples.
The web page http://matti.usu.edu/nlvm/nav/frames_asid_272_g_3_t_4.html
contains a simple applet that helps you practice using conversion factors and
their inverses.
|
|
|
2.3
|
Unit Conversion
|

|
|
|
|
When converting from one unit to another, we use the
unit identity that has the same unit in the denominator as the unit of the
unified quantity that it multiplies.
So if we want to convert the unified quantity "3 in" into
centimeters, we would multiply by the unit identity "2.54 cm/in"
which results in multiplying the quantity 3 by 2.54.
|

|
When do we multiply?
When do we divide?
|
On the other hand, if we want to convert "5 cm"
to inches, we would multiply by the unit identity "(1/2.54) in/cm"
which results in dividing the quantity 5 by 2.54. This idea is widely used in the physical sciences like physics
and chemistry to solve certain word problems, but we will now extend the idea
of unit conversions and cancellation to many other fields such as accounting,
finance, architecture, and home economics to name a few.
|
|
|
2.4
|
Proportionality
|

|
|
|
|

|

|
|
|
3 [in~Length(Fork)]
|
6 [in~Length(Fork)]
|
9 [in~Length(Fork)]
|
|
.2 [in~Width(Fork)]
|
.4 [in~Width(Fork)]
|
.6 [in~Width(Fork)]
|
|
3 / .2 = 15
|
6 / .4 = 15
|
9 / .6 = 15
|
|
|
|
2.5
|
Constant of Proportionality
|

|
|
|
3 [in~Length(Fork)] = 1/5
[in~Width(Fork)]
15 [in~Length(Fork)] /
[in~Width(Fork)]
(1/15) [in~Width(Fork)] /
[in~Length(Fork)]
|
One unified equation from a
proportional relationship
Constants of Proportionality
|
We use constants of proportionality similar to unit
identities. They convert dimensions as well as
units. For example, if we have a fork
that is proportional to these other forks but has a width of .5 inches, then
we calculate the length by multiplying it by the constant of proportionality
having width in denominator
Notice the key role that proportionality plays to allows
us to extend the idea of "equality" to unified quantities. Consider some unified equations and their
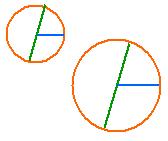
corresponding constants of proportionality for the thing "Circle".
|
2 [ft~Diameter(Circle)] = 1
[ft~Radius(Circle)]
2 [ft~Diameter(Circle)] /
[ft~Radius(Circle)]
π
[m~Circumference(Circle)] = 1 [m~Diameter(Circle)]
π [m~Circumference(Circle)] / [m~Diameter(Circle)]
|
|
Notice that the resulting ratios are not unit identities;
they are constants of proportionality.
On the other hand, a unit identity can be considered as a special case
of a constant of proportionality where the scaled dimensions only differ by
their units as illustrated below:
|
2.54 [cm~Length(Board)] = 1
[in~Length(Board)]
2.54 [cm~Length(Board)] /
[in~Length(Board)]
4 [cups~Volume(Jar)] = 1 [qt~Volume(Jar)]
4 [cups~Volume(Jar)] / [qt~Volume(Jar)]
|
Unit Identities are
Constants of Proportionality
|
|
|
|
2.6
|
Cancellation Rule
|

|
|
|

|
The inch (in) unit cancels
out leaving only "cm".
The centimeter (cm) unit
cancels leaving "in".
|
We can think of this process of multiplying by a unit
identity or constant of proportionality as a process of canceling units. When converting the unified quantity
"3 in" to centimeters, the inch (in) unit cancels. When converting the unified quantity
"5 cm" to inches the centimeter (cm) unit cancels.
|
When multiplying two
unified quantities, we can cancel matching units if one unified quantity is
a constant of proportionality with a denominator meaning that matches the
meaning of the other unified quantity.
|
|
|
|
|
2.7
|
Constant Rate
|

|
|
|
|
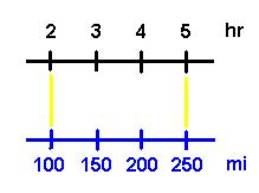
Consider the speed of a car as an example of rate. This rate is not constant when the car
accelerates; but after it reaches a cruising speed (a constant speed) then
we have a constant rate. At a
constant rate of 50 miles per hour (mi/hr), for example, if we change the
time of the trip from 2 hr to 5 hr (a difference of 3 hr) then the distance
will change from 100 mi (obtained from 50 mi/hr * 2 hr) to 250 mi (obtained
from 50 mi/hr * 5 hr), a difference of 150 mi. Notice that the constant rate of 50 mi/hr times the
difference of 3 hr does indeed give us the expected 150 mi.
|
[hr~
Time(Trip)]
[mi~
Length(Trip)]
|
|
[in~
Length(Thing)]

[cm~Length(Thing)]
|
Notice how the above diagram of the scaled dimensions
[hr~Time(Trip)] and [mi~Length(Trip)] parallel each other in the same
manner as centimeters and inches line up on a ruler.
|
|
In Unified Math® a rate expresses how a unified quantity
change as another unified quantity changes when the thing changes. In later chapters, we will present the
rate as a (derivative) function.
For now, we think of a constant rate as the constant of
proportionality between the changes in two proportional unified
quantities. By the cancellation
rule, if one quantity changes by a
certain amount, then the other quantity changes by that amount times the
constant of proportionality.
|
2 m/s
.5 s/m
60 mi/hr
7.95 dol/box
22 mi/gal
50 people/show
2.54 cm/in
3 ft/yd
|
Examples of Constant Rates
|
In general, a constant rate can multiply unified
quantities that have meanings that match the meaning in the denominator of
the rate and the cancellation rule apply.
|
2 m/s *10 s = 20 m
.5 s/m *20 m = 10 s
60 mi/hr *3 hr = 180 mi
7.95 dol/box *2 box = 15.90 dol
22 mi/gal *3 gal = 66 mi
50 people/show *4 show = 200 people
2.54 cm/in *1 in = 2.54 cm
3 ft/yd *200 yd = 600 ft
|
Multiplying constant rates
with abbreviated unified quantities
|
|
|
|
2.8
|
Unit Chains
|

|
|
|
|
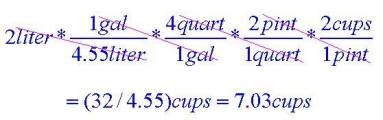
|
Unit Chain
|
To construct a unit chain, begin with a unified quantity
(like "2 liter" in this example) and repeatedly multiply by
constant rates (including unit identities and constants of proportionality)
where meaning in the numerator of the resulting unified quantity matches the
denominator of the next unified quantity being multiplied. The first multiplication in this example
matches the unit "liter" and the last multiplication matches the
unit "pint".
|
|
|
2.9
|
The Domino Strategy
|

|
|
|
|
Word Problem
|
Solution Using Units Analysis
|
|
What is the mass (in kilograms) of a person who weighs 180 pounds
(lb). (Hint: 1 lb = .453 kg)
|
x kg
= (.453 kg/ lb)
* 180 lb = 81.5 kg
|
If a word problems involves only multiplication and
division operators, one of the most effective solution strategy, which we
will call the domino
strategy, creates a chain of factors starting with a unified quantity
having the desired meaning (highlighted in yellow) in the numerator of its
meaning expression and continues to multiply by unified quantities that again
has a numerator meaning matching the previous denominator meaning. In such cases the factors usually involve
unit conversions and constant rates.
In the example above, we want to find kilograms (kg) so we start with
the unified quantity .453 kg/lb which has the unit kg in the numerator. Then we use the unit "lb" in the
numerator to select the next factor 180 lb.
The first factor in this example is a unit conversion. In this next example, the first factor
used is a constant of proportionality.
|
Word Problem
|
Solution Using Units Analysis
|
|
If the car can get 30 miles per gallon (mi/gal), what distance (in miles) can the car
travel before it runs out of 15 gallons?
|
x mi
= (30 mi/gal) *
15 gal = 450 mi
|
Here we desire the unit miles to begin the domino
strategy. We again can multiply by 15
gal to cancel out the unit "gal".
Go ahead and solve the following problems and check the answers below.
|
Word Problem
|
Solution Using Units Analysis
|
|
How many hours will it take a truck traveling 40 miles per hour to go
160 miles?
|
|
|
With a price of 2 dollars per quart, how many quarts can a person
buy with 30 dollars?
|
|
|
How much money do we need to purchase 3 liters (L) of chemicals if 2
gallons (gal) of chemicals cost 4 dollars (dol)? (Hint: 1 gal = 3.78
L)
|
|
|
How many seconds in a day?
|
|
|
How fast is a car going in miles per hour if the odometer reads 90
kilometers per hour? (Hint: 1.609 m
= 1 mi)
|
|
Here are some domino solutions for the above problems.
|
Word Problem
|
Solution Using Units Analysis
|
|
What is the mass (in kilograms) of a person who weighs 180 pounds
(lb). (Hint: 1 lb = .453 kg)
|
x kg
= (.453 kg/ lb)
* 180 lb = 81.5 kg
|
|
If the car can get 30 miles per gallon (mi/gal), what distance (in miles) can the car
travel before it runs out of 15 gallons?
|
x mi
= (30 mi/gal) *
15 gal = 450 mi
|
|
How many hours will it take a truck traveling 40 miles per hour to go
160 miles?
|
x hr
= (1 hr / 40
mi) * 160 mi = 4 hr
|
|
With a price of 2 dollars per quart, how many quarts can a person
buy with 30 dollars?
|
x qt = (1 qt
/ 2 dol) * 30 dol = 15 qt
|
|
How much money do we need to purchase 3 liters (L) of chemicals if 2
gallons (gal) of chemicals cost 4 dollars (dol)? (Hint: 1 gal = 3.78
L)
|
x dol
= (4 dol/2 gal)
* (1 gal/3.78 L) * 3 L = 22.68 dol
|
|
How many seconds in a day?
|
x s
= (60 s/min)*(60
min/hr)*(24 hr/d)* 1 d = 86400 s
|
|
How fast is a car going in miles per hour if the odometer reads 90
kilometers per hour? (Hint: 1.609 m
= 1 mi)
|
x mi/hr = (1 mi / 1.609 km)* (90 km/hr) = 56 mi/hr
|
|
|
|
2.10
|
Combining Proportional
Quantities
|

|
|
|
|
|
|
2.11
|
Activities and Explorations
|

|
|
|
|
|
Activities:
|
|
Practice Using Unit Identities
http://matti.usu.edu/nlvm/nav/frames_asid_272_g_3_t_4.html
Play “Unit Chain Gang” game
Play "Word Problem Torpedo" game
Each team takes turns creating a constant-rate word
problem (the torpedo) and fires it at the other team. The other team then attempts to solve.
Play "Recipe Swapping" game
Each team creates a (reasonable) recipe (either from
scratch or from ideas in recipe books) that contains at most ten
items. The teams swap recipes and
race to convert the recipes to the metric system. Each correct conversion gives that team a point. Each incorrect conversion gives the other
team that point.
|
Explorations:
Exercises:
|
|
Home
| Top
Copyright ©
2004 Dr. Ranel E. Erickson
|