Chapter 10.  Modeling Method

Step 1:  Identify quantities, dimensions, and things

Step 2:  Measurequantities with meaning expressions involving scaled dimensions

Step 3:  Relate the quantities (and add more meaningful quantities as needed)

Step 4:  Formulate a model

Step 5:  Solve the formulated model

Unified Math® approaches word problems with five systematic steps that unify meaning with quantities effectively.  We begin by taking these steps in the specified order, but often find ourselves returning back to previous steps to add more information so that we can proceed with later steps.  When implementing these steps, the meaning table finds not only the values requested in the problem, but the other related quantity values as well.

Using a simple rate word problem, let us investigate the five steps using a meaning table.

Step 1 - Identify:

The values entered into the first column determine one specific state of the system quantities labeled sequentially in the second column.  What those values mean and how they relate to each other appear in the other two columns.  Starting with the requested variable allows us to focus on those quantities related to the desired result.

Step 2 - Measure:

The unit to measure time is not explicitly given in the problem; but the units associated with 60 use the unit "hour", so we will use that unit to measure the time.  This also follows the basic principle of keeping the notation consistent.  These meaning expressions use standard unit abbreviations and dimensions as listed in Basic Algebra Vocabulary.  Even though this is not necessary, and we could have used “Distance” instead of “Length” and “miles” instead of “mi”, consistency will help us to solve much more complex problems.

Step 3 - Relate:

If we assume that the speed of the car remains constant (hence proportional), then the division of the scaled dimensions implies a direct division q3/q1 of the quantities q3 and q1.

Step 4 - Formulate:

The entries in the Value column and the Relationships columen equal the Quantity.  So we can obtain equations that relate the quantities:  t=q1, 60=q2=q3/q1, 240=q3

Step 5 - Solve:

Finally we solve the equations for solutions.  We use techniques that we will discuss in more detail in the last part of this book.  In this problem, we can substitute the known values for q1 and q3 into the relationship equation q2=q3/q1 from the second line in the meaning table:  60=240/t.  Then we isolate the variable t to get:  t=4.

No matter what abbreviation you use for the actual three components of meaning, use that notation consistently in all other meaning expressions.  Use enough information to completely distinguish a number.  So, for example, if you use the unit "lb" as an abbreviation with the number 18, you cannot have another number like 24 with only that unit.  This would result in an ambiguous situation, and by the algebraic nature of Unified Math®, 18 lb = 24 lb.  You would need to resolve this ambiguity explicitly mentioning the dimensions and/or things that the two different numbers refer to.

Furthermore, we encourage the consistent use of standard unit symbols and dimension words.  For example, if the problem discusses a fence around a rectangular yard, then use "Rectangle" as the thing and "Perimeter" as the dimension representing the fence.

Formulate::  60=240/t

Solve: t=4

Step 1:  Identify quantities, dimensions, and things

Step 2:  Measurequantities with meaning expressions involving scaled dimensions

Step 3:  Relate the quantities (and add more meaningful quantities as needed)

Step 4:  Formulate a model

Step 5:  Solve the formulated model

This abbreviated form uses just the units and substitutes the values immediately on building the relationships between the quantities.  An even shorter strategy uses unit analysis in Chapter 2 and yields:  t hr = 1hr/60mi * 240 mi = 4 hr; but this only works for problems involving only multiplication and division.  We went through all the steps, though, in this problem to help you begin to learn the general modeling method that works for practically all word problems involving units. 

Rather than use any abbreviations or shortcuts, we will walk through a detailed modeling process:

Step 1 - Identify

First let us identify some abstract things and dimensions that correspond to the volume of a pool.  In the abstract, the two-dimensional geometric shape above gives us the top and bottom surface of a solid object with 6 feet of height.  The dimension "volume" that we want to find depends (through multiplication) on the area of this surface and the height through which it projects.  So we can begin by identifying such quantities, where we use V to represent the quantity of volume and TA to represent total area covered by the pool as depicted in the irregular shape above.

Step 2 - Measure

As we identify these first few quantities associated with the desired result, we can also measure them by entering their meaning into the Meaning column.

Step 3 - Relate

By using the definition of volume of a solid, we have found two other related dimensions.  We can now enter that relationship into the Relationship column using the generic quantity variables q2 and q3.  This indicates that the first quantity q1 depends on the other two quantities.

Step 4 - Formulate

At any time along the development of a model, we can extract all the equations implied by each line in the meaning table and formulate the current model.  At this point we would have a general model:

V=q1=q2*q3

6=q2

TA=q3

Step 5 - Solve

If we attempt to solve the problem by substituting values and isolating variables we would end up with one equation V=6*TA that has two variables. 

We need more information to solve this problem. 

Many complex problems break up into smaller problems that together provide the answer to the complex problem.  In order to continue developing a model for this problem we need to find the area of a strange irregular shape.  How can we divide this shape into smaller shapes for which we can determine area?

One approach would extend the line marked with 35 over to the line marked with 40.  By doing this, we identify more dimensions (not even drawn originally) that help us break the shape up into more common shapes.  Remember, Euclid constructed most of geometry using simple shapes (including the circle, triangle, and rectangle) all of which have well known formulas for their areas.

When working with the meaning table, we can go back to previous steps and identify and measure other quantities as needed.  In this case, we need to determine the total area TA as the sum of two more quantities:  AT with dimension "the area of the triangle" and AR with dimension "the area of the rectangle".  In doing this we revisit Step 1 by identifying some more quantities and dimensions and revisit Step 2 by measuring these new quantities. 

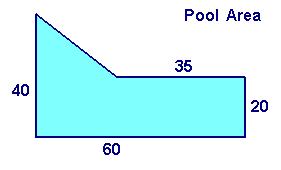
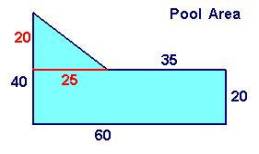
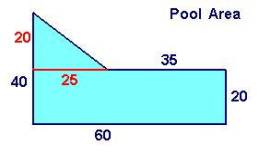
The last four quantities entered have meanings that directly relate to the definitions of the area dimensions for quantities AT and AR.  The measurements of these new dimensions relate to the originally measured dimensions.  Rather than list in the table all the numbers explicitly stated in the diagram, we enter those quantities related to our goal and measure them from general information in problem.

The previous table now shows 4 general relationships between the quantities in this system of things.  These equations hold true for any state of this particular type of thing, in this case, shape of a pool.  We now formulate a specific model by substituting the values of these quantities for a particular state of the system:

On substituting each of the values up into the first equation we can calculate the solution.

 Activities:

Explorations:

Exercises:

Home  |  Top

Copyright © 2004  Dr. Ranel E. Erickson