Chapter 3.  Abstraction

The concept of a "thing" comes from that which we experience in our lives.  Things include not only physical objects, but other concepts as well such as events in time, monetary transactions, software programs, etc.  In this book, we will focus on things that we can measure. 

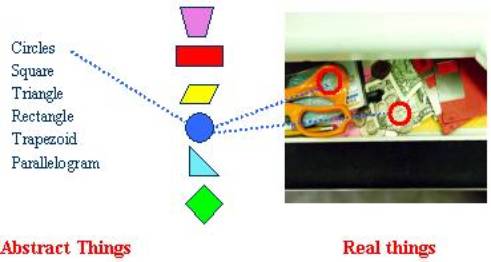
Abstract things help us to describe and relate real things.  The abstract concept of a circle can describe the shape of a coin or the hole in scissor handles,

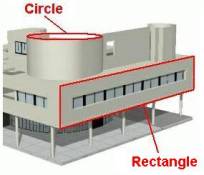
Things usually have many properties, and the properties that we can measure (with a unit scale) we call dimensions.  This includes not only geometric dimensions such as width, height, and depth; but also such dimensions as weight, temperature, cost, surface area, volume, speed, time, density, surface area, etc.  Note how the width, height, and depth dimensions of an appliance (like a washer machine) correspond to an abstract rectangular solid (a box) with minimal size to contain the appliance.

A triangle is an example of an abstract thing.  It has many related dimensions.  The dimensions listed here appear a basic algebra course.  But with a little bit of curiosity, browse through many other properties of triangles at http://mathworld.wolfram.com/Triangle.html.  It may surprise you how many dimensions you will find.  Similarly for dimensions of circles, check out http://mathworld.wolfram.com/Circle.html. 

In the 4-th century BC, a brilliant teacher Euclid set up a system of geometric objects in his famous work, The Elements.  In essence, he began with some basic shapes and construction concepts (points, lines, rays, circles, right angles, parallel lines) and then constructed and proved the field of classical geometry.  Used for over two millenniums as the primary resource for math education, The Elements presents logical arguments to construct many of the abstract things and relationships found in mathematics.  (http://aleph0.clarku.edu/~djoyce/java/elements/toc.html)

http://aleph0.clarku.edu/~djoyce/java/elements/bookI/propI1.html.

It is amazing how Euclid began with 23 definitions and 5 postulates in Book I and then proceeded to prove over 465 propositions beginning with such simple concepts of point, line, circle, and angle.   Indeed, geometry gives us many abstract shapes and relationships between those shapes that help us describe the world around us.  These basic shapes allow us to create many interesting geometric figures and properties.  Explore the interactive examples of constructions at the website:  http://www15.addr.com/~dscher/

Even today, geometry textbooks teach the concept of "proof", and build propositions and theorems based on assumed definitions and postulates.

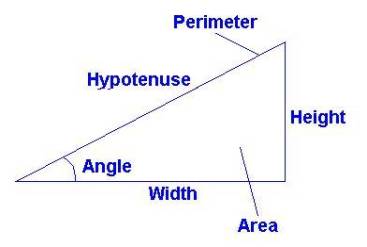
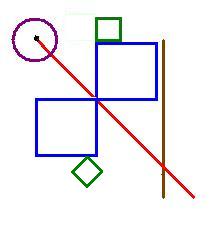
Certain words in the mathematical vocabulary describe shapes (figures) and the relationships between those geometric shapes.  In the above diagram, use the listed words to describe patterns that you see.  For resources to do this visit:  http://www.mathleague.com/help/geometry/coordinates.htm

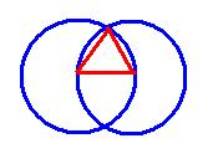
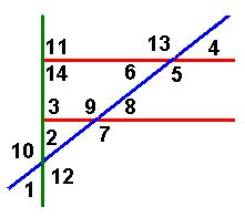
Certain words in the mathematical vocabulary describe types of angles and the relationships between angles.  The above diagram contains two horizontal parallel lines with two other lines, one perpendicular and one oblique (having a slant).  Use the listed words to describe relationships and patterns in this diagram.  For resources to do this visit:  http://www.mathleague.com/help/geometry/angles.htm

 Activities:

Explorations:

Exercises:

Home  |  Top

Copyright © 2004  Dr. Ranel E. Erickson